Найдём диагональ d прямоугольника-основания призмы как гипотенузу в прямоугольном треугольнике, образованном сторонами основания и его диагональю. Она является проекцией диагонали призмы на основание, а также катетом в прямоугольном треугольнике, образованном катетом - ребром призмы (равным высоте призмы) , катетом - диагональю основания и гипотенузой - диагональю призмы.
d=
Прямоугольный треугольник, в котором есть внутренний угол 45°, является равнобедренным, поэтому высота призмы равна диагонали основания, как два катета в равнобедренном прямоугольном треугольнике.
Площадь боковой поверхности узнаем, вычислив периметр основания и умножив его на высоту призмы.
280 см²
Объяснение:
Найдём диагональ d прямоугольника-основания призмы как гипотенузу в прямоугольном треугольнике, образованном сторонами основания и его диагональю. Она является проекцией диагонали призмы на основание, а также катетом в прямоугольном треугольнике, образованном катетом - ребром призмы (равным высоте призмы) , катетом - диагональю основания и гипотенузой - диагональю призмы.
d=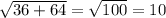
Прямоугольный треугольник, в котором есть внутренний угол 45°, является равнобедренным, поэтому высота призмы равна диагонали основания, как два катета в равнобедренном прямоугольном треугольнике.
Площадь боковой поверхности узнаем, вычислив периметр основания и умножив его на высоту призмы.
Sбок.=P·d=(6+8)·2·10=280 см²
Две боковые грани: ABS и ADS - перпендикулярны плоскости основания.
Средние по величине боковые ребра BS и DS равны 15.
Находим высоту пирамиды.
Плоскость средних рёбер проходит через диагональ BD основания, середина которой - точка О. BD = 12√2.
Отрезок SО равен √(15² - (6√2)²) = √(225 - 72) = √153.
Тогда высота Н пирамиды равна: Н = √(153 - 72) = √81 = 9.
Определяем координаты вершин пирамиды.
A(0; 0; 0), B(0; 12; 0), C(12; 12; 0), D(12; 0; 0), S(0; 0; 9).
1. Нахождение длин ребер и координат векторов:
x y z Длина ребра
Вектор АВ={xB-xA, yB-yA, zB-zA} 0 12 0 12
Вектор BC={xC-xB, yC-yB, zC-zB} 12 0 0 12
Вектор АD={xD-xA, yD-yA, zD-zA} 12 0 0 12
Вектор CD={xD-xC, yD-yC, zD-zC} 0 -12 0 12
Вектор АS={xS-xA, yS-yA, zS-zA} 0 0 9 9
Вектор BS={xS-xB, yS-yB, zS-zB} 0 -12 9 15
Вектор CS={xS-xC, yS-yC, zS-zC} -12 -12 9 19,20937271
Вектор DS={xS-xD, yS-yD, zS-zD} -12 0 9 15.
2. Площади граней
a1 a2 a3 S
ABCD AB^2 144
ABS [AB; AS]= 108 0 0 54
BCS [BC; BS]= 0 -108 -144 90
CDS [CD; CS]= -108 0 -144 90
ADS [AD; AS]= 0 -108 0 54
Sпол = 432, Sбок =288.
Произведение векторов a × b = {aybz - azby; azbx - axbz; axby - aybx}.
ответ: Sбок =288 (площади можно находить по формуле Герона).