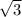решить задачу ортогональной проекцией треугольника ABC на некоторою плоскость является прямоугольный равнобедренный треугольник a1 b1 c1 если площадь равна 12 см найди угол между плоскостями ABC и a1 b1 c1 если площадь треугольника ABC равна 72 см в квадрате
2) Неверно, касательной называется прямая, которая имеет с окружностью только одну общую точку, если точек две - имеем дело с хордой;
3) Верно, центр вписанной окружности равноудалён от сторон треугольника - все точки равноудалённые от сторон угла принадлежат биссектрисе угла, место пересечения биссектрис равноудалено от всех сторон треугольника - значит центр вписанной окружности;
4) Верно, здесь небольшая логическая ловушка: описанная окружность обязательно проходит через все три вершины треугольника, утверждение "хотя бы две" является включением в первое высказывание - тоже истинно.
ответ: 134.
ответ: Диаметр самая длинная хорда в окружности, запомните это дети! И ешьте манную кашу!
Объяснение:
АО = ОВ = 5, тогда радиус равен АО = ОС = 10. Отрезок ВС = 15.
Если хорда пересекается диаметром перпендикулярно, то хорда делится пополам, поэтому DB=BE.
Хорды в точке пересечения делятся на отрезки так, что произведение отрезков одной хорды равно произведению отрезков второй.
То есть, DB*DE = AB*BC отсюда DC²= 5*15 = 75, DC = 5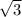
По теореме Пифагора, DC² = DB²+BC². И подставив значения найдем, что DC = 10