решить задачу с первого равенства треугольников

Высота, опущенная на гипотенузу прямоугольного треугольника, равна 3, биссектриса прямого угла равна 4. Найдите площадь треугольника.

ответ: 72 (ед. площади)

Объяснение:

∆ АВС, угол С=90°, высота СН =3, биссектриса СК=4.

Решение.

Из ⊿ СНК: sin ∠СКН=СН:СК=3/4=0,75 ⇒

∠СКН=48,59° - внешний ∆ АСК ⇒

∠САК=48,59°-∠АСК=48,59°-45=3,59°

∠СВА=90°-3,59°=86,4°

Из ⊿ АСН гипотенуза АС=СН:sinCAK=3:0,0626=47,9108

Из ⊿ СВН гипотенуза СВ=СН:sin CBH=3:0,998=3.006

Площадь прямоугольного треугольника равна половине произведения катетов.

S (ABC)=AC•BC=47,9108•3,006=72,009 ≈ 72 (ед. площади)

(см. объяснение)

Объяснение:

1)

Пусть диагональ правильного пятиугольника равна a, а боковая сторона b.

Тогда по теореме косинусов:

Золотое сечение - это .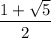

Полученные значения не равны, поэтому утверждение неверное.

Правильное утверждение:

Диагонали правильного пятиугольника пересекаются и точкой пересечения делят друг друга на отрезки, связанные между собой золотым сечением.

2)

Очевидно, что утверждение ложное!

Правильное утверждение:

Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.

ИЛИ

Диагонали ромба/квадрата являются биссектрисами его внутренних углов.

3)

Также сразу понятно, что утверждение верное!