ответ: Б.) 52/4=13 см сторона ромба10:2=5 см половина диагонали ромба13*13=169 квадрат стороны 5*5=25 квадрат половины диагонали169-25=144 квадрат половины другой диагоналиКорень из 144 равен 12 см - половина второй диагонали12*2=24 см вторая диагональ
А.) А) треугольник АОВ прямоугольный, и АО = одна вторая АС, ВО = одна вторая ВD. Значит АО = 3дм а ВО = 4дм. По теореме Пифагора АВ = корень квадратный из 3 во второй степени + 4 во второй степени = корень квадратный из 9 + 16 = корень квадратный из 2
Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что,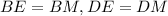 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что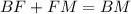 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть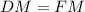 .
.
Учитывая доказанные равенства получаем,
Что требовалось доказать.
ответ: Б.) 52/4=13 см сторона ромба10:2=5 см половина диагонали ромба13*13=169 квадрат стороны 5*5=25 квадрат половины диагонали169-25=144 квадрат половины другой диагоналиКорень из 144 равен 12 см - половина второй диагонали12*2=24 см вторая диагональ
А.) А) треугольник АОВ прямоугольный, и АО = одна вторая АС, ВО = одна вторая ВD. Значит АО = 3дм а ВО = 4дм. По теореме Пифагора АВ = корень квадратный из 3 во второй степени + 4 во второй степени = корень квадратный из 9 + 16 = корень квадратный из 2