Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S = (дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
Zmeura1204
Объяснение:
1)
Дано:
АВСD-параллелограм
AB=10см
AD=15см
<А=30°
S=?
_______
Решение
S=AB*AD*sin<A
sin<30°=1/2
S=1/2*10*15=75см²
ответ: 75см²
2)
Дано:
ABCD- трапеция
<ВАD=<ABC=90°
<BCD=135°
BC=2см
АВ=2см
S(ABCD)=?
______
Решение
Сумма углов прилежащих к боковой стороне трапеции равна 180°
<CDK=180°-<BCD=180°-135°=45°
Проведём высоту СК.
∆CKD- прямоугольный равнобедренный треугольник (углы при основании равны. <СКD=90°; <CDK=45°; <KCD=90°-45°=45°)
CK=KD=AB=2см
АD=BC+KD=2+2=4см.
S(ABCD)=CK(BC+AD)/2=2(2+4)/2=6см²
ответ: 6см²
32дм²
Объяснение:
Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S =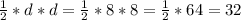 (дм²)
(дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
x² + x² = 8²
2x² = 64
x² = 32
x = √32 = √16*2 = 4√2 (дм)
Площадь квадрата x², то есть площадь равна 32дм²