Стороны данного треугольника равны 15 см, 20 см, 30 см. Найдите стороны треугольника с периметром 26 см, подобного данному треугольнику. Покажите, что отношение площадей треугольников ABC и A1B1C1 равно (3)
Объяснение:
Т.к. стороны ΔАВС равны 15 см, 20 см, 30 см , то отношение этих сторон 3:4:6. Такое же отношение сторон будет и в подобном ΔА₁В₁С₁.
Пусть одна часть сторон ΔА₁В₁С₁ будет х , тогда длина сторон будет равна 3х, 4х,6х.
Стороны данного треугольника равны 15 см, 20 см, 30 см. Найдите стороны треугольника с периметром 26 см, подобного данному треугольнику. Покажите, что отношение площадей треугольников ABC и A1B1C1 равно (3)
Объяснение:
Т.к. стороны ΔАВС равны 15 см, 20 см, 30 см , то отношение этих сторон 3:4:6. Такое же отношение сторон будет и в подобном ΔА₁В₁С₁.
Пусть одна часть сторон ΔА₁В₁С₁ будет х , тогда длина сторон будет равна 3х, 4х,6х.
Т.к. Р(А₁В₁С₁) =26 см , то 3х+ 4х +6х =26 , х=2.
Тогда стороны ΔА₁В₁С₁ такие 6 см ,8 см ,12 см.
Найдем коэффициент подобия к=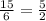
.
По т. об отношении площадей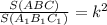
,получаем
А 3 не получается.
Объяснение:
1) Дано △MPR - равносторонний, TR=8, TR-высота.
Решение: Поскольку △MPR - равносторонний, то MR=MP=PR=x. TR - высота, она же для равност. тр-ка медиана, поэтому PT=x/2. По теореме Пифагора
2) Дано ABCD - прямоугольник, AC=26, AD=10.
Решение: По теореме Пифагора находим сторону CD:
3) Дано △MNS - прямоугольный, MN=2√3, <NMS=30°.
Решение: cosNMS=
4) Дано △KEF - прямоугольный, EL - высота из вершины E, EK=9, EF=12.
Решение: По теореме Пифагора найдём
Рассмотрим △KLE. В нём sinK=x/EK=x/9. А для △KEF, sinK=EF/KF=12/15
Таким образом