У колі з радіусами АО і ОВ пряма а проходить через середини радіусів так, що ОЕ = ОА/4. Оскільки відстань - це перпендикуляр, маємо прямокутний трикутник КОЕ та РОЕ. З прямокутного трикутника КОЕ: ОК = ОА/2, ОЕ = ОА/4. Тобто, катет ОЕ у два рази менший за гіпотенузу ОК. Катет, що дорівнює половині гіпотенузи, лежить проти кута 30 градусів. Тобто, кут ОКЕ = 30 градусів. Кут КОЕ = 90 - 30 = 60 градусів. Трикутники КОЕ та РОЕ рівні за прямим кутом та гіпотенузою, тобто кути КОЕ та РОЕ рівні і дорівнюють по 60 градусів. Кут АОВ = <KOE + <POE = 60 + 60 = 120 градусів.
1) Пусть дана равнобедренная трапеция АВСД (АД - большее основание, ВС -меньшее). Тогда по условию разность углов С и А равна 36. Но угол С = угол В (равнобед).
Значит В-А=36. По свойству односторонних углов А+В=180. Решаем систему
Больший угол равен 108.
2) По теореме косинусов 25+9-2*5*3*(-0,5)=49.
Значит, АС=7.
3) Рисунок к задаче во вложении. Извиняюсь за качество - рисовал на планшете.
Угол АВД=69-вписанный равен половине дуги АД, дуга АД = 2*69=138.
Угол САД=67-вписанный равен половине дуги СД, дуга СД = 2*67=134.
Угол АВС-вписанный равен половине дуги АС=АД+ДС, дуга АС =138+134=272.
1) Пусть дана равнобедренная трапеция АВСД (АД - большее основание, ВС -меньшее). Тогда по условию разность углов С и А равна 36. Но угол С = угол В (равнобед).
Значит В-А=36. По свойству односторонних углов А+В=180. Решаем систему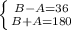
Больший угол равен 108.
2) По теореме косинусов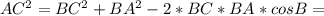
25+9-2*5*3*(-0,5)=49.
Значит, АС=7.
3) Рисунок к задаче во вложении. Извиняюсь за качество - рисовал на планшете.
Угол АВД=69-вписанный равен половине дуги АД, дуга АД = 2*69=138.
Угол САД=67-вписанный равен половине дуги СД, дуга СД = 2*67=134.
Угол АВС-вписанный равен половине дуги АС=АД+ДС, дуга АС =138+134=272.
Значит, угол АВС=272:2=136.