Решите с 4 по 6 (у меня есть этот же во и там + к 71,ответы одинаковые если решите)

Показать ответ

Ответ:

ALIONA2020

06.09.2021 01:12

а) ∠В = 30°, АВ=4 см, AD=ВD=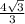 $\frac{4\sqrt{3} }{3}$ см ∠D=120°

б) S = 2√3 cм²

Объяснение:

а) Сумма острых углов прямоугольного треугольника равна 90°

∠В=90°-∠А=90°-60°=30°

Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.

⇒ АВ=2*АС=2*2=4см

По теореме Пифагора найдём катет ВС:

$BC=\sqrt{AB^{2}-AC^{2} } =\sqrt{4^{2}-2^{2} } =\sqrt{12} =2\sqrt{3}$

ВС = 2√3 см

Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.

$\dfrac{AB}{BC} =\dfrac{BD}{DC} \\\\\\\dfrac{4}{2} =\dfrac{BD}{2\sqrt{3}-BD } \\\\\\BD=4\sqrt{3} -2BD\\\\3BD=4\sqrt{3} \\\\BD=\dfrac{4\sqrt{3} }{3}$

Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=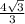 $\frac{4\sqrt{3} }{3}$ см

Так как сумма углов треугольника = 180°, то

∠АDB = 180-∠ВАD-∠В=180-30-30=120°

б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:

$S = \dfrac{1}{2} *BC*AC=\dfrac{1}{2} *2\sqrt{3} *2=2\sqrt{3}$

S = 2√3 cм²

В треугольнике ABC ∠C = 90°, AD – биссектриса, ∠A = 60°, AC = 2 см. а) Решите треугольник ABD ( ). б

0,0(0 оценок)

Ответ:

evgenscorp1

27.07.2020 04:32

Проведем радиусы от центра окружности О до точек касания В и С. И соедини центр окружности с точкой А.
рассмотрим получившиеся треугольники АВО и АСО, в них:
угол АВО = угол АСО = 90 гр. (св-во касательных) , следовательно, треугольники АВО и АСО прямоугольные. А чтобы доказать равенство двух прямоуг. треуг-ов достаточно найти 2 равных элемента:
- катет ОВ = катет ОС (радиусы окружности)
- ОА - общ. гипотенуза
из этого следует, что треугольники равны, следовательно все элементы этих треуг-ов равны. а следовательно равны и катеты АС и АВ
ч. т. д.

0,0(0 оценок)

Популярные вопросы: Геометрия