Решите с полным оформлением, всё таки , тут теоремы и множество прелестей. 1. в прямоугольнике abcd сторона ab=3, bc=4. окружности вписаны в треугольники abc и adc. найдите расстояние между их центрами. 2. длины диагоналей ромба относятся как 3: 5. найдите отношение площади ромба к площади вписанного в него круга.

Проведем высоту к основанию равнобедренного треугольника. Высота поделит основание на две равные части, т.е. 18/2=9.

Когда мы провели высоту (она же медиана, кстати), у нас образовалось два прямоугольных треугольника. Э ти треугольники будут равны, т.к. гипотенузы уних и катеты равны.

Площадь одного треугольника найдем по теореме Пифагора

41^2=9^2(половина основания большого треугольника)+x^2(х- высота)

х=40.

40 и 9 - катеты тр. S= половина произведения катетов (40*9)/2=180.

Т.к. прямоугольные тр. равны, то площадь большого треугольника равна: 2*180=360.

ответ:360!

Доказательство:

Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.

Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.

Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что, .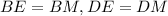

Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что .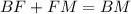

Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть .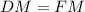

Учитывая доказанные равенства получаем,

Что требовалось доказать.