Расстояние от моста до пристани катер преодолел на 2 часа быстрее, чем расстояние от пристани до моста. Найдите собственную скорость катера, если скорость течения 2 км/ч, а расстояние между пристанью и мостом 48 км.
Объяснение:
Пусть собственная скорость катера х км/ч , х>0,
тогда скорость катера против течения (х-2) км/ч. ,
а скорость по течению (х+2) км/ч .
Время катера против течения 48/(х-2) ч,
а время катера по течению 48/(х+2) км/ч.
Т.к время катера против течения на 2 часа больше , то составим уравнение : ,
Возможно (и скорее всего), не самый короткий путь, но всё же.
Рассмотрим тр-ки △ANC и △CMA. У них АС - общая, <NAC=<MCA как углы при основании равнобедренного △ABC, а <ACN=<CAM как половинки этих равных углов (поскольку AM и CN - биссетрисы). => △ANC=△CMA по 2му признаку.
Из равенства △ANC=△CMA следует, что AN=CM. Очевидно также что и BN=BM
По обратной теореме Фалеса Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.
Значит АС || MN => <AMN=<MAC как внутренние накрест лежащие (секущая AM). А <BMN=<MCA как соответственные (секущая ВС). При этом <AMN=<MAC=1/2<NAC=1/2<MCA => <BMN=2<AMN. Что и требовалось доказать.
Расстояние от моста до пристани катер преодолел на 2 часа быстрее, чем расстояние от пристани до моста. Найдите собственную скорость катера, если скорость течения 2 км/ч, а расстояние между пристанью и мостом 48 км.
Объяснение:
Пусть собственная скорость катера х км/ч , х>0,
тогда скорость катера против течения (х-2) км/ч. ,
а скорость по течению (х+2) км/ч .
Время катера против течения 48/(х-2) ч,
а время катера по течению 48/(х+2) км/ч.
Т.к время катера против течения на 2 часа больше , то составим уравнение :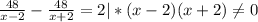 ,
,
48(х+2)-48(х-2)=2(х-2)(х+2) ,
49х+96-48х+96=2х²-8,
2х²=192+8,
х²=100 ⇒ х=10.
ответ. Собственная скорость катера 10 км/ч.
Объяснение:
Возможно (и скорее всего), не самый короткий путь, но всё же.
Рассмотрим тр-ки △ANC и △CMA. У них АС - общая, <NAC=<MCA как углы при основании равнобедренного △ABC, а <ACN=<CAM как половинки этих равных углов (поскольку AM и CN - биссетрисы). => △ANC=△CMA по 2му признаку.
Из равенства △ANC=△CMA следует, что AN=CM. Очевидно также что и BN=BM
По обратной теореме Фалеса Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.
Значит АС || MN => <AMN=<MAC как внутренние накрест лежащие (секущая AM). А <BMN=<MCA как соответственные (секущая ВС). При этом <AMN=<MAC=1/2<NAC=1/2<MCA => <BMN=2<AMN. Что и требовалось доказать.