192. Диагонали параллелограмма пересекаются и точкой пересечения О делятся пополам. Треугольники АВС и АДС равновеликие (равны по площади); треугольники АОД и СОД тоже равновеликие; треугольники АОК и КОД тоже равновеликие. Следовательно, если SАДС=1/2отSАВСД, то SАОД=SСОД=1/4отSАВСД. А SКОД=1/8отSАВСД. В сумме SСОД и SКОД=3/8отSАВСД. То есть отношение 3:8.
193. Большая сторона - гипотенуза (5х). Катеты соответственно равны 4х и 3х. Треугольники, образованные высотой, прямоугольные. Все три подобны между собой. Составим пропорцию на основе подобия треугольников: ; ; . Если х=10, то гипотенуза =10*5=50, катеты: 10*4=40, 10*3=30. Периметр P=50+40+30=120.
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Доказательство.
Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны. Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку. Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1. Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана. 53 Нравится
192. Диагонали параллелограмма пересекаются и точкой пересечения О делятся пополам. Треугольники АВС и АДС равновеликие (равны по площади); треугольники АОД и СОД тоже равновеликие; треугольники АОК и КОД тоже равновеликие. Следовательно, если SАДС=1/2отSАВСД, то SАОД=SСОД=1/4отSАВСД. А SКОД=1/8отSАВСД. В сумме SСОД и SКОД=3/8отSАВСД. То есть отношение 3:8.
193. Большая сторона - гипотенуза (5х). Катеты соответственно равны 4х и 3х. Треугольники, образованные высотой, прямоугольные. Все три подобны между собой. Составим пропорцию на основе подобия треугольников: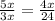
; 
; 
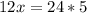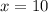. Если х=10, то гипотенуза =10*5=50, катеты: 10*4=40, 10*3=30. Периметр P=50+40+30=120.
Доказательство.
Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны.
Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку.
Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1.
Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана. 53 Нравится