Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её ). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме и , то есть
Найди площадь фигуры, заданной на координатной плоскости.
Объяснение:
Разобьем данную фигуру прямыми на 3 прямоугольника.
S(1)=АВ*ВН , длина отрезка АВ=-7-(-15)=-7+15=8,
длина отрезка ВН= 18-(-11)=18+11=29.
S(1)=8*29=232(ед²).
S(2)=КС*КР , длина отрезка КС=-15-(-28)=-15+28=13,
длина отрезка КР= 10-(-11)=10+11=21.
S(2)=13*21=273(ед²).
S(3)=МТ*МН , длина отрезка МТ=8-(-7)=8+7=15,
длина отрезка МН= 6-(-11)=6+11=17.
S(3)=15*17=255(ед²).
S(фигуры)=232+273+255=760(ед²)
242
Объяснение:
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её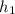 ). Тогда справедливо следующее равенство:
). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме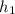 и
и 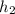 , то есть
, то есть