через две пересекающиеся прямые проходит плоскость, и притом только одна.
прямые l и m пересекаются, следовательно, лежат в одной плоскости а₁в₁в₂а₂.
из свойства параллельных плоскостей:
линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
отрезки а₁в₁ и а₂в₂ параллельны, т.к. лежат в параллельных плоскостях α и β и являются линиями пересечения этих плоскостей с плоскостью а₁в₁в₂а₂..
в ∆ а₁ов₁ и ∆ а₁ов₁ углы при о равны как вертикальные, и углы при а₁в₁ и а₂в₂ равны как накрестлежащие при пересечении параллельных прямых секущими l и m
следовательно,
треугольники ∆ а₁ов₁ и ∆ а₂ов₂ подобны по равенству углов.
ответ:
по следствию 2 из аксиомы 1 стереометрии:
через две пересекающиеся прямые проходит плоскость, и притом только одна.
прямые l и m пересекаются, следовательно, лежат в одной плоскости а₁в₁в₂а₂.
из свойства параллельных плоскостей:
линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
отрезки а₁в₁ и а₂в₂ параллельны, т.к. лежат в параллельных плоскостях α и β и являются линиями пересечения этих плоскостей с плоскостью а₁в₁в₂а₂..
в ∆ а₁ов₁ и ∆ а₁ов₁ углы при о равны как вертикальные, и углы при а₁в₁ и а₂в₂ равны как накрестлежащие при пересечении параллельных прямых секущими l и m
следовательно,
треугольники ∆ а₁ов₁ и ∆ а₂ов₂ подобны по равенству углов.
тогда отношение а₁в₁: а₂в₂=3: 4.
12: а₂в₂=3/4
3 а₂в₂=48 см
а₂в₂=16 см
Обозначим пирамиду МАВС, МО - высота пирамиды. МО перпендикулярна основанию пирамиды.
О - центр описанной окружности около основания АВС данной пирамиды.
Все углы правильного треугольника равны 60°. По т.синусов радиус АО описанной окружности равен
R=AO:2sin60°
Если условие задано верно и сторона основания равна 4, то:
Тогда по т.Пифагора из прямоугольного ∆ АМО высота
МО=√(AM²-AO²)=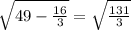
Но эта задача обычно задается со стороной основания, равной 4,5
Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту.
Для этого значения
R=4: 2√3/2=4,5:√3=1,5•√3
По т.Пифагора высота пирамиды
МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)