радиус ОА, проведённый к точке касания В образует с ней прямой угол 90°. Поэтому ∆ОВN-прямоугольный. По условиям ОВ=1,5см, а ON=2см. По теореме Пифагора найдём BN:
BN=2²-(1,5)²=√(4-2,25)=√1,75; BN=√1,75
Задание 2:
Так как радиус ОА, проведённый к точке касания В образует с ней прямой угол 90°, то ∆ОВС-прямоугольный. По условиям угол С = 90°, а значит этот треугольник равнобедренный, поскольку в прямоугольном равнобедренном треугольнике оба острых угла равен каждый по 45°, и значит ВС=ВО=5см;
Объяснение: задание 1
радиус ОА, проведённый к точке касания В образует с ней прямой угол 90°. Поэтому ∆ОВN-прямоугольный. По условиям ОВ=1,5см, а ON=2см. По теореме Пифагора найдём BN:
BN=2²-(1,5)²=√(4-2,25)=√1,75; BN=√1,75
Задание 2:
Так как радиус ОА, проведённый к точке касания В образует с ней прямой угол 90°, то ∆ОВС-прямоугольный. По условиям угол С = 90°, а значит этот треугольник равнобедренный, поскольку в прямоугольном равнобедренном треугольнике оба острых угла равен каждый по 45°, и значит ВС=ВО=5см;
ответ: ВО=5см
ответ: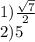
Объяснение: