Формула объёма пирамиды: V=(1/3)*S*H S - площадь основания H - высота пирамиды
Так как нам известно, что в основании лежит прямоугольник, а его стороны 6 и 7, то сразу найдём площадь основания: S=a*b=6*7=42
Теперь нужно найти высоту. Для этого нам нужно найти диагональ прямоугольника. Воспользуемся теоремой Пифагора d=√(7²+6²)=√85
Теперь рассмотрим треугольник, образованный высотой пирамиды, её гранью и половиной диагонали основания. С теоремы Пифагора найдём высоту H=√(13²-(√(85)/2)²)=√111 V=(1/3)*42*√111=14√111
Дано: АВСД - трапеция, ВС=12 см, АД=18 см, АС- биссектриса угла А
Найти S трапеции
1) ВС||АД, АС - секущая. Значит ∠ВСА=∠САД как накрест лежащие.
2) ∠ВАС=∠САD , потому что АС- биссектриса.
∠ВСА=∠САД как накрест лежащие. (см. пункт 1)
Отсюда следует, что ∠ВАС=∠ВСА.
3) Рассмотрим треугольнике АВС. Он равнобедренный, так ка углы при основании равны.(∠А=∠С из пункта 2). Значит АВ=ВС=12 см
4) Рассмотрим ΔАВН. ВН- высота, АВ=12 см, АН=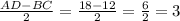
см. Этот треугольник прямоугольный, поэтому по теореме Пифагора найдём катет ВН
ВН=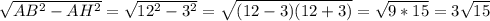
см
5) Найдем площадь трапеции
V=(1/3)*S*H
S - площадь основания
H - высота пирамиды
Так как нам известно, что в основании лежит прямоугольник, а его стороны 6 и 7, то сразу найдём площадь основания:
S=a*b=6*7=42
Теперь нужно найти высоту. Для этого нам нужно найти диагональ прямоугольника. Воспользуемся теоремой Пифагора
d=√(7²+6²)=√85
Теперь рассмотрим треугольник, образованный высотой пирамиды, её гранью и половиной диагонали основания. С теоремы Пифагора найдём высоту
H=√(13²-(√(85)/2)²)=√111
V=(1/3)*42*√111=14√111