На стороне AB равностороннего треугольника ABC взята точка D так, что сумма расстояний от нее до сторон AC и BC равна 16 см. Найдите высоту треугольника, проведенную из вершины C.
РЕШЕНИЕ: Пусть сторона треугольника а. Одно из данных расстояний m, другое – n. Расстояния – это высоты. Находим площади треугольников:
Сюда относится картинка с умножением
Теперь их суммируем:
Сюда с сложением
В левой части полная площадь ABC, правую можно периписать так:
Сюда с сложением и умножением
Где h - высота из вершины C, равна сумме расстояний = 16 см
Обозначим пирамиду SABCD, В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны, вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей. Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.
Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒ 0,5d=5•1/√3, d=10/√3, S=0,5•(10/√3)²= ед. площади.
На стороне AB равностороннего треугольника ABC взята точка D так, что сумма расстояний от нее до сторон AC и BC равна 16 см. Найдите высоту треугольника, проведенную из вершины C.
РЕШЕНИЕ: Пусть сторона треугольника а. Одно из данных расстояний m, другое – n. Расстояния – это высоты. Находим площади треугольников:
Сюда относится картинка с умножением
Теперь их суммируем:
Сюда с сложением
В левой части полная площадь ABC, правую можно периписать так:
Сюда с сложением и умножением
Где h - высота из вершины C, равна сумме расстояний = 16 см
ОТВЕТ: 16 см
Обозначим пирамиду SABCD, В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны, вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей. Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.
Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒ 0,5d=5•1/√3, d=10/√3, S=0,5•(10/√3)²=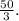
ед. площади.