Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 = = 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3
Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 =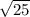 = 5
= 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3
Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 =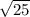 = 5
= 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3