1. Неверно - в р.б трапеции углы должны быть равными при одном основании, но т.к в условии этого не указано, то к этому утверждению можно отнести прямоугольную трапецию. 2. Неверно - один из неизвестных углов может быть тупым
рассмотрим два случая, например, с углом в 40* а) угол в 40* находится при основании, тогда: второй угол при основании тоже 40* угол напротив основания: 180-40*20=100* он тупой(больше 90*) б) угол в 40* находится напротив основания, тогда: углы при основании равны: (180-40)/2=70* 3.Неверно - вписанный угол в два раза меньше центрального, опирающегося на ту же дугу. 4.Неверно - центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. 5. Неверно - потому что в ромбе может не соблюдаться основное условие: около выпуклого четырёхугольника можно описать окружность только тогда, когда сумма его противоположных углов равна 180°. 6. Неверно - только если это не квадрат, только в этом прямоугольнике стороны будут касаться окружности. 7. Верно - в параллелограмме противоположные углы равны, а сумма углов при одной какой то стороне равна 180*.
2. Неверно - один из неизвестных углов может быть тупым
рассмотрим два случая, например, с углом в 40*
а) угол в 40* находится при основании, тогда:
второй угол при основании тоже 40*
угол напротив основания:
180-40*20=100* он тупой(больше 90*)
б) угол в 40* находится напротив основания, тогда:
углы при основании равны:
(180-40)/2=70*
3.Неверно - вписанный угол в два раза меньше центрального, опирающегося на ту же дугу.
4.Неверно - центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
5. Неверно - потому что в ромбе может не соблюдаться основное условие:
около выпуклого четырёхугольника можно описать окружность только тогда, когда сумма его противоположных углов равна 180°.
6. Неверно - только если это не квадрат, только в этом прямоугольнике стороны будут касаться окружности.
7. Верно - в параллелограмме противоположные углы равны, а сумма углов при одной какой то стороне равна 180*.
Обозначим пирамиду МАВС, МО - высота пирамиды. МО перпендикулярна основанию пирамиды.
О - центр описанной окружности около основания АВС данной пирамиды.
Все углы правильного треугольника равны 60°. По т.синусов радиус АО описанной окружности равен
R=AO:2sin60°
Если условие задано верно и сторона основания равна 4, то:
Тогда по т.Пифагора из прямоугольного ∆ АМО высота
МО=√(AM²-AO²)=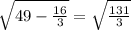
Но эта задача обычно задается со стороной основания, равной 4,5
Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту.
Для этого значения
R=4: 2√3/2=4,5:√3=1,5•√3
По т.Пифагора высота пирамиды
МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)