Сім ребер чотирикутної піраміди мають однакову довжину , а восьме ребро обрано так, щоб об’єм піраміди мав максимальне значення. знайти об’єм цієї піраміди.
Пусть пирамида называется ABCDE, где Е - верхняя точка, ABCD - квадрат-основание. Теорема Пифагора наше всё. Сначала проводим диагональ BD в основании-квадрате и по теореме находим гипотенузу (а2+б2=с2), а и б равно 1, подставляем в формулу - получается диагональ равна "корень из 2". проводим высоту в пирамиде (EF, где F - точка на диагноали BD). Эта высота будет также и медианой в равностороннем треугольнике BED, деля нашу гипотенузу BD на 2, т.е. длина отрезков BF и FD будет равно "корень из 2"/2. у нас образовался треугольник EBF. BE=1, BF тоже известно. снова пользуемся теоремой пифагора для данного треугольника и находим высоту. По моим расчетам получилось 1/(корень из 2)
Пусть ВС = a, AD = b, и пусть h – высота трапеции (см. рисунок)
По свойству (диагонали трапеции разбивают её на четыре треугольника с общей вершиной, площади треугольников, прилежащих к боковым сторонам, равны.) S(ABO)=S(CDO) , обозначим эту площадь S0 (действительно, S (ABD) = S(ACD) , т. к. у них общие основания и равные высоты, т. е. S(AOB)+S(AOD)=S(COD)+S(AOD) откуда следует S(AOB) =S(COD)).
Так как S(ABC)= S0+ S1= h*a/2 и S(ACD)= S0+ S2= h*b/2 , то (S0+S1)/(S0+S2)=a/b
Далее, треугольники BOC и DOA подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит S1/S2=(a/b)^2
Таким образом, (S0+S1)/(S0+S2) =
Отсюда находим S1= =36/9=4
Поэтому площадь трапеции будет равна s= S1+S2+2S0= 4+9+12=25
Теорема Пифагора наше всё. Сначала проводим диагональ BD в основании-квадрате и по теореме находим гипотенузу (а2+б2=с2), а и б равно 1, подставляем в формулу - получается диагональ равна "корень из 2". проводим высоту в пирамиде (EF, где F - точка на диагноали BD). Эта высота будет также и медианой в равностороннем треугольнике BED, деля нашу гипотенузу BD на 2, т.е. длина отрезков BF и FD будет равно "корень из 2"/2.
у нас образовался треугольник EBF. BE=1, BF тоже известно. снова пользуемся теоремой пифагора для данного треугольника и находим высоту. По моим расчетам получилось 1/(корень из 2)
По свойству (диагонали трапеции разбивают её на четыре треугольника с общей вершиной, площади треугольников, прилежащих к боковым сторонам, равны.) S(ABO)=S(CDO) , обозначим эту площадь S0 (действительно, S (ABD) = S(ACD) , т. к. у них общие основания и равные высоты, т. е. S(AOB)+S(AOD)=S(COD)+S(AOD) откуда следует S(AOB) =S(COD)).
Так как S(ABC)= S0+ S1= h*a/2 и S(ACD)= S0+ S2= h*b/2 , то (S0+S1)/(S0+S2)=a/b
Далее, треугольники BOC и DOA подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит S1/S2=(a/b)^2
Таким образом, (S0+S1)/(S0+S2) =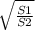
Отсюда находим S1=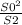
=36/9=4
Поэтому площадь трапеции будет равна s= S1+S2+2S0= 4+9+12=25