с Сором ! 2.Найдите координаты точек, симметричных точкам М(-6;8) и К(0;-2) относительно: 1)оси абсцисс 2)оси ординат.
3.Треугольник АВС имеет вершины А(2;1), В(3;6), С(-1;-3).Этот треугольник отображается в треугольник МЕF относительно точки D(-5;3). Найдите координаты вершин М,Е,F.
4.В системе координат нарисуй треугольник АВС с координатами вершин: А(-1;-1),В(-4,9;-1),С(-1;-4,9). Нарисуй треугольник А¹В¹С¹,полученный при повороте треугольника АВС вокруг начала координат на 180°. Нарисуй треугольник А²В²С² полученный в симметрии треугольника А¹В¹С¹ относительно прямой х=0. Определи Координаты:А²В²С².
Расстояние от точки K до прямой MN - отрезок FK, равный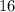 (см).
(см).
Объяснение:
1. Рассмотрим равносторонний ΔMNK:
Т.к. ΔMNK - равносторонний, то каждый угол будет равняться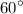 .
.
По условию из точки K к отрезку MN проведём биссектрису KF, которая по свойству делит ∠K на два равных угла.
⇒ ∠NKF = ∠FKM = 60° : 2 = 30°.
Расстояние от точки до прямой/отрезка - перпендикуляр.
⇒ Проводим из вершины F перпендикуляр к отрезку MK, равный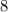 (см).
(см).
Благодаря этому перпендикуляру, получаем прямоугольный ΔFGK с прямым углом G (оставшиеся два угла - острые).
2. Рассмотрим прямоугольный ΔFGK:
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет FG в 2 раза меньше гипотенузы FK, т.е. FK =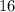 (см).
(см).
Т.к. ΔMNK - равносторонний ⇒ он является и равнобедренным с основанием NM.
Биссектриса, проведённая к основанию равнобедренного треугольника, является и высотой, и медианой.
⇒ биссектриса FK - высота треугольника MNK, и в тоже время перпендикуляр к прямой MN.
⇒ отрезок FK - расстояние от точки K до прямой MN.
ΔMNQ: по теореме косинусов:
MQ² = MN² + NQ² - 2 · MN · NQ · cos45°
MQ² = (3√2)² + 7² - 2 · 3√2 · 7 · √2/2 = 18 + 49 - 42 = 25
MQ = 5 см
ΔMNQ = ΔMNP по двум сторонам и углу между ними (NQ = NP по условию, MN - общая, ∠MNQ = ∠MNP по условию), ⇒
MP = MQ = 5 см
ΔMPQ: p = (5 + 5 + 8)/2 = 9 см
по формуле Герона:
Smpq = √(p · (p - MP) · (p - MQ) · (p - PQ))
Smpq = √(9 · (9 - 5) · (9 - 5) · (9 - 8)) = √(9 · 4 · 4 · 1) = 3 · 4 = 12 см²