Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса:
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
⇒ h = OO₁ = BH = 24 см
ответ: h = 24 см
P.S. Рисунок показан внизу↓
Объяснение:
Найдем сторону с по углу и двум прилежащим сторонам:
с=√a²+b²-2ab*cos30° = 8²+9² -2*8*9*0.866=64 + 81 - 124,704 = 20.296≈20.3;
По теореме синусов
a/sinA = b/sinB=c/sin С
a/sinA=c/sinC;
SinA=a*sinC/c=8*0.5/20.3=0.197;
∠A=11.36°
∠B=180° - (∠A+∠C) = 180° - (30°+11.36°) = 180° - 41.36° = 138.64°
***
2. По теореме синусов
a/sinA = b/sinB=c/sin С. ∠C=90°. a=12; c=13.
sinA=a*sinC/c=12* 1 /13= 0.923;
∠A=67.4°;
∠B= 180° - (∠A+∠С) = 180° - (67,4° + 90°) = 180° -157,4° = 22,6°
∠B=22.6°
Найдем сторону b по углу и двум прилежащим сторонам:
b=√a²+c²-2ac*cos22.6°=√12²+13²-2*12*13*0,923= √144+169 - 287,976 = 25.
Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: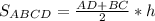
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
ответ: h = 24 см
P.S. Рисунок показан внизу↓
Объяснение:
Найдем сторону с по углу и двум прилежащим сторонам:
с=√a²+b²-2ab*cos30° = 8²+9² -2*8*9*0.866=64 + 81 - 124,704 = 20.296≈20.3;
По теореме синусов
a/sinA = b/sinB=c/sin С
a/sinA=c/sinC;
SinA=a*sinC/c=8*0.5/20.3=0.197;
∠A=11.36°
∠B=180° - (∠A+∠C) = 180° - (30°+11.36°) = 180° - 41.36° = 138.64°
***
2. По теореме синусов
a/sinA = b/sinB=c/sin С. ∠C=90°. a=12; c=13.
sinA=a*sinC/c=12* 1 /13= 0.923;
∠A=67.4°;
∠B= 180° - (∠A+∠С) = 180° - (67,4° + 90°) = 180° -157,4° = 22,6°
∠B=22.6°
Найдем сторону b по углу и двум прилежащим сторонам:
b=√a²+c²-2ac*cos22.6°=√12²+13²-2*12*13*0,923= √144+169 - 287,976 = 25.