с задачами:
1) Площадь параллелограмма равна 75 см2 , а одна из его сторон равна 15 см. Найти высоту параллелограмма, проведенную к этой стороне.
2) Основание равнобедренного треугольника равно 14 см, а боковая сторона равна 16см. Найти площадь треугольника.
3) Боковая сторона трапеции образует с основанием угол 30 градусов, а высота трапеции равна два корня из трех см. Найти площадь трапеции, если в нее можно вписать окружность.
4) Найти площадь ромба, сторона которого равна 26см, а разность диагоналей равна 28см.
5) Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки равные 20см и 15 см. Найти площадь треугольника.
Сейчас напишу
Объяснение:
1.Площадь параллелограмма =сторона *высота,сторона =15 см,значит высота= площадь/сторону=75см2/15=5см
2..Построим треугольник пусть АВС.Проведем в нем высоту ВН,получился прямоугольный треугольник(т.к высота перпендикулярна основанию и образует угол 90 градусов),в нем гипотенуза АВ=16 см,один из катетов=половине стороны АС т.к треугольник равнобедренный и высота является медианой(т.е 14/2)=7см
По теореме пифагора найдём второй катет,т.е высоту трегольника АС:
АВ^2=ВН^2+АН^2
16^2=7^2+BH^2
256=49+BH^2
256-49=207
ВН=√207≈14,39
Площадь треугольника=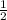 аh(половина основания на высоту)=14см/2*14,39=7*14,39=100.73см2
аh(половина основания на высоту)=14см/2*14,39=7*14,39=100.73см2
3.Построим трапецию АВСД .В трапецию можно вписать окружность,когда суммы противолежащих сторон в ней равны и трапеция равнобокая.Площадь трапеции равна S=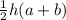
Проведём высоту.Она=2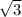 .Образовался прямоугольный треугольник.Высота(дана)также является катетом.Она лежит против угла в 30 градусов,значит по теореме она равна половине гипотенузы.Гипотенузой здесь является боковая сторона.Она равна 2*высоту=2
.Образовался прямоугольный треугольник.Высота(дана)также является катетом.Она лежит против угла в 30 градусов,значит по теореме она равна половине гипотенузы.Гипотенузой здесь является боковая сторона.Она равна 2*высоту=2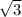 *2= 4
*2= 4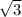 .
.
Так как трапеция равнобокая то сумма боковых сторон=4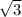 *2=16
*2=16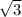 .Суммы оснований такие же.Найдем площадь:
.Суммы оснований такие же.Найдем площадь:
=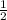 *2
*2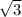 *16
*16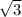 =3*16=48см2
=3*16=48см2
Остальное не вышло(