Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что . Проведем прямую . Тогда . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. , а значит и любой прямой в этой плоскости. Пусть . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость . Покажем, что . и , и . Тогда задача сводится к нахождению площади треугольника . Будем искать ее, как . Из подобия треугольников следует, что . Из подобия треугольников . Подставив найденное в формулу выше, получим . Таким нами образом было получено, что искомая площадь равна .
Так как отрезанная часть пирамиды подобна целой и коэффициент подобия равен 2, то верхнее основание усеченной пирамиды равно S2=S1/2=600/2=300 см².
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S2 (abc), нижнего основания усеченной пирамиды S1 (ABC) и средней пропорциональной между ними.
(см. объяснение)
Объяснение:
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что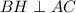 . Проведем прямую
. Проведем прямую  . Тогда
. Тогда 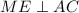 . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е.
. Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. 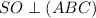 , а значит и любой прямой в этой плоскости. Пусть
, а значит и любой прямой в этой плоскости. Пусть  . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда
. Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда 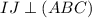 , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость
, а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость 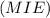 . Покажем, что
. Покажем, что 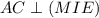 .
. 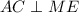 и
и 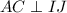 , и
, и 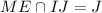 . Тогда задача сводится к нахождению площади треугольника
. Тогда задача сводится к нахождению площади треугольника 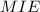 . Будем искать ее, как
. Будем искать ее, как 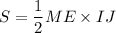 . Из подобия треугольников следует, что
. Из подобия треугольников следует, что 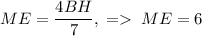 . Из подобия треугольников
. Из подобия треугольников 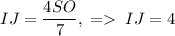 . Подставив найденное в формулу выше, получим
. Подставив найденное в формулу выше, получим 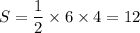 . Таким нами образом было получено, что искомая площадь равна
. Таким нами образом было получено, что искомая площадь равна 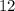 .
.
Задание выполнено!
ответ: 8828,4 см³.
Объяснение:
По формуле Герона
S осн=√p(p-a)(p-b)(p-c), где
p=(a+b+c)/2=(25+29+36)/2=45 см.
S1=√45(45-25)(45-29)(45-20)=√360000 =600 см²;
Так как отрезанная часть пирамиды подобна целой и коэффициент подобия равен 2, то верхнее основание усеченной пирамиды равно S2=S1/2=600/2=300 см².
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S2 (abc), нижнего основания усеченной пирамиды S1 (ABC) и средней пропорциональной между ними.
V=⅓H(S₁+√(S₁S₂)+S₂) =1/3*20(300+√(300*600)+600)=8828,4 см³.