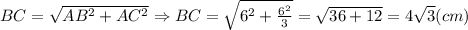Самостоятельная работа.

Перечертить чертежи в тетрадь. Условие записывать не нужно, решение с подробными пояснениями записать ОБЯЗАТЕЛЬНО!

Во всех задачах нужно найти расстояние от точки М до прямой АВ.

(Расстоянием от точки до прямой называют длину перпендикуляра проведенного из этой точки к данной прямой)

Задача 1

задача 2

задача 3

задача 4

1)начнем с того, что это равнобедренная трапеция. углы при основаниях равны. то есть угол а=в=(360-120*2)/2=60 градусов; d=c=120 градусов.
2)затем делаем дополнительные построения -высота dh и ck перпендикулярные ab, тогда ah=kb=14-8/2=3
3)теперь рассматриваем отдельно треугольник adh:
уголahd=90(dh-высота)
угол dah=60
сумма всех углов =180, тогда угол adh=180-90-60=30
4) рассмотрим опять этот треугольник угол adh=30
сторона ah=3, тогда ad=ah*2(катет прямоугольного треугольника лежащий против угла в 30 градусов равен половине гипотенузы)
и получается, что ad=cb=6.
отсюда - периметр равен сумме всех сторон, то есть 8+14+6+6=34

см

Объяснение:

Побудуємо прямокутний ΔАВС, з висотою АК=3 см і гострим ∠В=30°.

І варіант рішення:

1) Розглянемо прямокутний ΔКВА.

Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)

Катет ВК=АК/tg(B) ⇒ BK=3√3 (см)

2) Трикутники АВС, КВА та КАС подібні між собою (за гострим кутом як прямокутні трикутники). Тому

ІІ варіант рішення:

1)  Розглянемо прямокутний ΔКВА.

Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)

2)  Розглянемо прямокутний ΔКАС.

В ньому ∠С=180°-90°-∠В=60°.

Гіпотенуза АС=АК/sin(С) ⇒ АС=3*2/√3=6/√3 (см)

3)  Розглянемо ΔАВС.

Гіпотенуза