В трапецию ABCD с основаниями BC и AD вписана окружность с центром в точке 0. Площадь Δ АОВ относится к площади Δ COD как 1:3. Тогда отношение sin A: sinD равно... .
Объяснение:
Центр вписанной окружности O лежит в точке пересечения биссектрис углов трапеции. Соединим т. О с точкой касания окружности с боковыми сторонами . Это будет радиус и высота ΔАОВ и ΔCOD ( кстати, прямоугольных) .
S(AOB)=0,5*AB*r ,S(COD)=0,5*CD*r . Тогда отношение
Объяснение:
Хорошо, могу объяснить. Мне не сложно)
Необходимым и достаточным условием существования треугольника является выполнение следующих неравенств: a+b>c, a+c>b, b+c>a, (a>0, b>0, c>0),
где a, b и с - длины сторон треугольника.
1) 3см,10см,5см.
3 + 5 > 12;
3+12 >5
5+12 >3
Первое неравенство неверно, следовательно, треугольника со сторонами 3см, 10см и 5см не существует.
2.12 см, 16 см,13 см
12+16>13
12+13>16
16+13>12 Все неравенства верны, следовательно, треугольник со сторонами 12см, 16см и 13см существует.
3.23см,27см,23см
23+27>23
23+23>27
27+23>23
Все неравенства верны, следовательно, треугольник со сторонами 23см, 27 см и 23см существует.
4.7см,21см,14см
7+21>14
7+14>21
21+14>7
Первое неравенство принимает вид равенства, следовательно, такой треугольник существует, но он вырожденный (все его вершины лежат на одной прямой).
В трапецию ABCD с основаниями BC и AD вписана окружность с центром в точке 0. Площадь Δ АОВ относится к площади Δ COD как 1:3. Тогда отношение sin A: sinD равно... .
Объяснение:
Центр вписанной окружности O лежит в точке пересечения биссектрис углов трапеции. Соединим т. О с точкой касания окружности с боковыми сторонами . Это будет радиус и высота ΔАОВ и ΔCOD ( кстати, прямоугольных) .
S(AOB)=0,5*AB*r ,S(COD)=0,5*CD*r . Тогда отношение
Пусть ВК⊥АD ,СР⊥АD. BK=CP =h
ΔABK-прямоугольный ,sin A=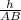 .
.
ΔDCP-прямоугольный ,sin D=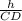 .
.
Отношение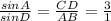 .
.