В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
=√147 см
Боковые грани правильной пирамиды это равные треугольники.
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=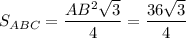
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=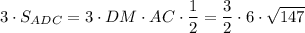
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
№2
Sabc=1/2 * АС*ВД
АС=6+4=10 см
ВД=ДС=4 см, т.к. ΔВДС - р/б; ∠С=45°; ∠СВД=90-45=45°
S=1/2 * 10 * 4=20 cм².
№3
Р=20 см; сторона а=5 см
Пусть х и у - половины диагоналей
х+у=14 : 2=7 см
Если одна половина диагонали = х, то вторая (7-х)
Рассм. один из 4-х маленьких прямоугольных треугольников, на которые диагонали делят ромб.
Катеты х и (7-х); гипотенуза а=5 см. По т.Пифагора
5²=х²+(7-х)²
х²+49-14х+х²-25=0
2х²-14х+24=0
х²-7х+12=0
D=49-4*1*12=1
х1=(7+1)/2=4 см, тогда у1=7-4=3 и наоборот.
Диагонали: 8 и 6 см
S=1/2 * 8 * 6=4*6=24 cм² - это ответ.