ответ: АС=170 см , R=106,25 см .
АВСД - равнобокая трапеция , ВК⊥АД , СН⊥АД , ВК=СН=80 см .
АД=210 см , ВС=90 см . Найти: АС и R .
Так как трапеция равнобокая, то АВ=СД ⇒ ΔАВК=ΔСНД ( по двум катетам : АВ=СД и ВК=СН как высоты) ⇒ АК=НД
АК=НД=(АД-КН):2=(АД-ВС):2=(210-90):2=60 см (КН=ВС как противоположные стороны прямоугольника КВСН ) .
Тогда из ΔСНД имеем СД=√(СН²+НД²)=√(6400+3600)=100 см
ΔАСД: S(ΔАСД)=0,5·АД·СН=0,5*210*80=8400 см²
Радиус окружности, описанной около трапеции, тот же самый, что и
радиус окружности, описанной около ΔАСД. А для радиуса описанной около треугольника окружности известна формула ⇒ .
В ΔАСД нам неизвестна только третья сторона АС, которая является диагональю трапеции .
Найдём её из ΔАСН. ∠АНС=90° , АН=АК+КН=АК+ВС=60+90=150 см
АС=√(АН²+СН²)=√(150²+80²)=√28900=170 см
см .
Объяснение:
а)
Обозначим высоту трапеции ВЕ=80 см.
Рассмотрим треугольник АВЕ.
ВЕ=80 см;
АЕ=(AD-BC)/2=(210-90)/2=120/2=60 (см).
АВ²=ВЕ²+АЕ²=80²+60²=6400+3600=10000.
АВ=√10000=100 (см).
В равнобедренной трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенное произведение оснований трапеции:
AC²+BD²=AB²+CD²+2*BC*AD
AC=BD AB=CD ⇒
2*AC²=2*AB²+2*BC*AD |÷2
AC²=AB²+2*BC*AD=100²+90*210=10000+18900=28900.
AC=√28900=170 (cм).
ответ: АС=170 см.
b)
где а - большее основание трапеции,
с - боковая сторона трапеции,
d₁ - диагональ трапеции.
ответ: R≈106,25 см.
ответ: АС=170 см , R=106,25 см .
АВСД - равнобокая трапеция , ВК⊥АД , СН⊥АД , ВК=СН=80 см .
АД=210 см , ВС=90 см . Найти: АС и R .
Так как трапеция равнобокая, то АВ=СД ⇒ ΔАВК=ΔСНД ( по двум катетам : АВ=СД и ВК=СН как высоты) ⇒ АК=НД
АК=НД=(АД-КН):2=(АД-ВС):2=(210-90):2=60 см (КН=ВС как противоположные стороны прямоугольника КВСН ) .
Тогда из ΔСНД имеем СД=√(СН²+НД²)=√(6400+3600)=100 см
ΔАСД: S(ΔАСД)=0,5·АД·СН=0,5*210*80=8400 см²
Радиус окружности, описанной около трапеции, тот же самый, что и
радиус окружности, описанной около ΔАСД. А для радиуса описанной около треугольника окружности известна формула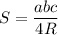 ⇒
⇒ 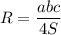 .
.
В ΔАСД нам неизвестна только третья сторона АС, которая является диагональю трапеции .
Найдём её из ΔАСН. ∠АНС=90° , АН=АК+КН=АК+ВС=60+90=150 см
АС=√(АН²+СН²)=√(150²+80²)=√28900=170 см
Объяснение:
а)
Обозначим высоту трапеции ВЕ=80 см.
Рассмотрим треугольник АВЕ.
ВЕ=80 см;
АЕ=(AD-BC)/2=(210-90)/2=120/2=60 (см).
АВ²=ВЕ²+АЕ²=80²+60²=6400+3600=10000.
АВ=√10000=100 (см).
В равнобедренной трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенное произведение оснований трапеции:
AC²+BD²=AB²+CD²+2*BC*AD
AC=BD AB=CD ⇒
2*AC²=2*AB²+2*BC*AD |÷2
AC²=AB²+2*BC*AD=100²+90*210=10000+18900=28900.
AC=√28900=170 (cм).
ответ: АС=170 см.
b)
где а - большее основание трапеции,
с - боковая сторона трапеции,
d₁ - диагональ трапеции.
ответ: R≈106,25 см.