Если две прямые перпендикулярны третьей, то они параллельны между собой.
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.
Теорема Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Объяснение:Основанием прямой призмы является равнобедренный прямоугольный треугольник. Большая боковая грань-квадрат со стороной 6 корней из 2 см.
а) найдите площадь полной поверхности этой призмы;
б) постройте сечение призмы плоскостью, проходящей через катет нижнего основания и середину противолежащего бокового ребра;
в) вычислите площадь этого сечения;
г) найдите угол между плоскостью сечения и плоскостью нижнего основания;
д) постройте линию пересечения секущей плоскости верхнего основания.
рисунок к задаче 190а) Призма прямая, т.е. её боковые ребра перпендикулярны основаниям. Боковые грани являются прямоугольниками. Площадь прямоугольника равна произведению длин смежных сторон, следовательно, площадь той грани больше, ребра которой больше. Боковые ребра параллелепипеда равны, а в основании самуую большую длину имеет гипотенуза, поэтому большая грань - ABB1A1.
И раз эта грань - квадрат, то все её стороны по 6 корней из 2, в том числе и гипотенуза основания. Пусть АС=ВС=х, из теоремы Пифагора найдем катеты основания и его площадь:
площадь основания
Теперь найдем площади боковых граней, а затем и площадь полной поверхности
KK₁ = 3 ед.
Объяснение:
Дано: прямая АВ;
АК=КВ;
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.
АА₁ = 5; ВВ₁ = 11.
Найти: КК₁
Пусть А₁В₁= 2а.
Если две прямые перпендикулярны третьей, то они параллельны между собой.
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.
Теорема Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
АК = КВ ⇒ А₁К₁ = К₁В₁ = а.
Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.
Вертикальные угла равны.
∠1 = ∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔОВВ₁ (по двум углам)
Составим пропорцию:
Пусть А₁О = 5х, тогда ОВ₁ = 11х
Составим уравнение:
⇒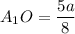
Тогда
Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.
∠1=∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔК₁КО
Составим пропорцию:
Объяснение:Основанием прямой призмы является равнобедренный прямоугольный треугольник. Большая боковая грань-квадрат со стороной 6 корней из 2 см.
а) найдите площадь полной поверхности этой призмы;
б) постройте сечение призмы плоскостью, проходящей через катет нижнего основания и середину противолежащего бокового ребра;
в) вычислите площадь этого сечения;
г) найдите угол между плоскостью сечения и плоскостью нижнего основания;
д) постройте линию пересечения секущей плоскости верхнего основания.
рисунок к задаче 190а) Призма прямая, т.е. её боковые ребра перпендикулярны основаниям. Боковые грани являются прямоугольниками. Площадь прямоугольника равна произведению длин смежных сторон, следовательно, площадь той грани больше, ребра которой больше. Боковые ребра параллелепипеда равны, а в основании самуую большую длину имеет гипотенуза, поэтому большая грань - ABB1A1.
И раз эта грань - квадрат, то все её стороны по 6 корней из 2, в том числе и гипотенуза основания. Пусть АС=ВС=х, из теоремы Пифагора найдем катеты основания и его площадь:
площадь основания
Теперь найдем площади боковых граней, а затем и площадь полной поверхности
нашли полную поверхность