Силы P = 100 H и F = 200 H приложены к некоторой материальной точке. Угол между векторами, изображающими эти силы, равен 50°. Найдите с точностью до 1 H равнодействующую сил P и F.
24. Проведём общую касательную к окружностям в точке O. Для меньшей окружности угол между касательной и хордой OC равен половине дуги OC, то есть равен вписанному углу ∠OBC. Для большей окружности угол между касательной и хордой OC₁ равен половине дуги OC₁, то есть равен вписанному углу ∠OB₁C₁. Поскольку хорды OC и OC₁ лежат на одной прямой, угол между касательной и этими хордами один и тот же. Углы ∠OBC и ∠OB₁C₁ равны одному и тому же углу, значит, они равны между собой. Тогда BC || B₁C₁.
По теореме синусов . Поскольку радиусы не равны, то и BC ≠ B₁C₁.
Противолежащие стороны четырёхугольника параллельны и не равны, следовательно, это трапеция, что и требовалось доказать.
25. Продлим биссектрису DF до пересечения с прямой BC (точку пересечения обозначим S), проведём высоту CH в треугольнике DCS. Обозначим площади следующим образом: .
Заметим, что ∠ADS = ∠DSC как накрест лежащие, ∠ADS = ∠SDC по условию. Тогда ∠DSC = ∠SDC ⇒ треугольник DCS равнобедренный ⇒ DH = HS.
Треугольники ADF и BSF подобны по вертикальным углам ∠AFD и ∠BFS и накрест лежащим углам ∠ADF и ∠FSB с коэффициентом подобия k = AF : FB = 2. Тогда и DF : FS = 2, а .
Треугольники CHS и BFS подобны по общему углу ∠S и соответственным прямым углам ∠CHS и ∠BFS. Коэффициент подобия . Тогда .
ответ:Противоположные стороны параллелограмма равны между собой
Одна сторона 2Х
Вторая 3Х
2Х•2+3Х•2=50
10X=50
X=5
Одна сторона 5•2=10 см
Вторая сторона 5•3=15 см
Проведём высоту,высота отсекла от параллелограмма прямоугольный треугольник с гипотенузой 10 см и острым углом 30 градусов
Катет треугольника,он же высота параллелограмма ,лежит против угла 30 градусов и поэтому в два раза меньше гипотенузы
10:2=5 см
Площадь параллелограмма-произведение высоты на сторону на которую высота опущена
S=5•15=75 см^2
Объяснение:
25. 7 : 8
Объяснение:
24. Проведём общую касательную к окружностям в точке O. Для меньшей окружности угол между касательной и хордой OC равен половине дуги OC, то есть равен вписанному углу ∠OBC. Для большей окружности угол между касательной и хордой OC₁ равен половине дуги OC₁, то есть равен вписанному углу ∠OB₁C₁. Поскольку хорды OC и OC₁ лежат на одной прямой, угол между касательной и этими хордами один и тот же. Углы ∠OBC и ∠OB₁C₁ равны одному и тому же углу, значит, они равны между собой. Тогда BC || B₁C₁.
По теореме синусов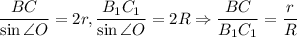 . Поскольку радиусы не равны, то и BC ≠ B₁C₁.
. Поскольку радиусы не равны, то и BC ≠ B₁C₁.
Противолежащие стороны четырёхугольника параллельны и не равны, следовательно, это трапеция, что и требовалось доказать.
25. Продлим биссектрису DF до пересечения с прямой BC (точку пересечения обозначим S), проведём высоту CH в треугольнике DCS. Обозначим площади следующим образом: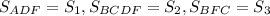 .
.
Заметим, что ∠ADS = ∠DSC как накрест лежащие, ∠ADS = ∠SDC по условию. Тогда ∠DSC = ∠SDC ⇒ треугольник DCS равнобедренный ⇒ DH = HS.
Треугольники ADF и BSF подобны по вертикальным углам ∠AFD и ∠BFS и накрест лежащим углам ∠ADF и ∠FSB с коэффициентом подобия k = AF : FB = 2. Тогда и DF : FS = 2, а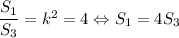 .
.
Треугольники CHS и BFS подобны по общему углу ∠S и соответственным прямым углам ∠CHS и ∠BFS. Коэффициент подобия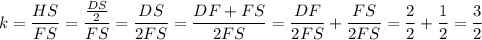 . Тогда
. Тогда 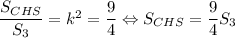 .
.
CH — медиана треугольника DCS, значит,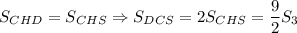 . Но
. Но 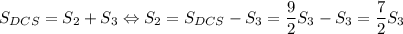 .
.
Искомое отношение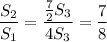 .
.