Обозначим пирамиду SABCD, В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны, вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей. Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.
Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒ 0,5d=5•1/√3, d=10/√3, S=0,5•(10/√3)²= ед. площади.
Площадь треугольника равна половине произведения его основания на высоту. вывод: S∆=0,5AB*CH, где АСВ - треугольник с основанием АВ и высотой СН. получить эту формулу можно с достроения треугольника до параллелограмма так, чтобы высота треугольника являлась и высотой параллелограмма, тогда площадь параллелограмм будет равна AB*CH, что равно 2S∆ABC, т.е площадь ∆ABC действительно равна 0,5AB*CH следствие 1: площадь прямоугольного треугольника равна половине произведения его катетов. следствие 2: если высоты двух треугольников равны, то и площади их относятся как основания. формулу Герона смотри во вложении.
Обозначим пирамиду SABCD, В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны, вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей. Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.
Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒ 0,5d=5•1/√3, d=10/√3, S=0,5•(10/√3)²=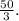
ед. площади.
следствие 1: площадь прямоугольного треугольника равна половине произведения его катетов.
следствие 2: если высоты двух треугольников равны, то и площади их относятся как основания.
формулу Герона смотри во вложении.