Маємо трапецію АБСД , де основи 16 і44 , а бічні сторони 17 і 25 , щоб знайти площу , треба мати висоту і знайти її в такій трапеції непросто.Проведемо дві висоти з вершини В та з С і позначимо першу ВК , а другу СЕ, ВК=СЕ і тоді знайдемо її методом порівняння.Позначимо відрізок АК через х. Знайдемо висоту ВК ВК²=17²-х² Далі знайдемо висоту СЕ , яка дорівнює ВК і порівняємо їх
СЕ²=25²-(28+х)² маємо: 17²-х²=25²-(28+х)² розвяжемо це рівняння х² скоротиться і ми отримаємо такий вираз:56х=448 х=8 , маючи Х (відрізок АК) знайдемо висоту ВК ВК²=17²-8²=225 ВК=15 Далі знайдемо площу трапеції S трап.= 16+44/2*15= 450(см²)
Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)
В итоге, формула линейной функции получится следующей:
450см²
Объяснение:
Маємо трапецію АБСД , де основи 16 і44 , а бічні сторони 17 і 25 , щоб знайти площу , треба мати висоту і знайти її в такій трапеції непросто.Проведемо дві висоти з вершини В та з С і позначимо першу ВК , а другу СЕ, ВК=СЕ і тоді знайдемо її методом порівняння.Позначимо відрізок АК через х. Знайдемо висоту ВК ВК²=17²-х² Далі знайдемо висоту СЕ , яка дорівнює ВК і порівняємо їх
СЕ²=25²-(28+х)² маємо: 17²-х²=25²-(28+х)² розвяжемо це рівняння х² скоротиться і ми отримаємо такий вираз:56х=448 х=8 , маючи Х (відрізок АК) знайдемо висоту ВК ВК²=17²-8²=225 ВК=15 Далі знайдемо площу трапеції S трап.= 16+44/2*15= 450(см²)
Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы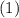
выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)В итоге, формула линейной функции получится следующей: