Составить каноническое уравнение эллипса, если сумма полуосей равна 7, а разность равна 1. Вычислить эксцентриситет.

1. проводим прямму а (базовое построение)

2. обозначем точку А на пряммой а (базовое построение)

3. Через точку А проводим пряммую с, перпендикулярную пряммой а (базовая задача на построение)

4. Откладываем от точки А отрезки АС и АВ длиной равные данному отрезку 1. (базовое построени). Получим прямоугольный треугольник, гипотенуза которого равна ВС=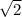

5. Продолжаем отрезок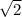 от точки С на отрезок равный данному, получим большой отрезок длинной ВР=1+\sqrt{2} (базовое построение)

6. На єтой же пряммой далее от точки Р откладываем отрезок РК равный данному с длиной 1.

7. Делим отрезок ВК пополам (базовая задача на построение)

8. Из середины О отрезка ВК радиусом ВО проводим окружность (базовое построение)

9. Через точку Р проводим перпендикулярную пряммую РХ,(базовая задача на построение) она пересечет окружность в двух точках, берем одну из них обозначаем Н,

отрезок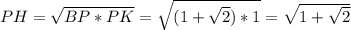 искомый

ответ:    S біч = ( 24 + 12√2 ) см² .

Объяснение:

В паралелепіпеді ABCD - паралелограм ; ∠А = 45° ; АВ =2√2 см ;

AD = 4 cм ; AC₁ = 7 см ;  S біч - ?          S біч= P * H ;

P = 2( 2√2 + 4 ) см .  У паралелограмі ABCD  ∠В = 180° - ∠А = 180°- 45°=

= 135° .  Із ΔАВС  за Т . косинусів : АС = √[(2√2)²+ 4² -2√2* 4cos135°] =

= √ ( 8 + 16 + 16√2cos45°) = √ ( 24 + 16√2 * √2/2 ) = √ 40 = 2√10 ( см ) .

Із прямок . ΔАСС₁ за Т . Піфагора  СС₁ = Н = √ (7² - ( 2√10 )² ) =

= √ (49 - 40 ) = √9 = 3 ( см ) .

S біч = ( 4√2 + 8 ) * 3 = ( 24 + 12√2 ) ( см² ) .