г). [Сначала разберем общий случай] Найдем максимальное количество прямых, которое можно провести через определенные n точек, никакие три из которых не лежат на одной прямой.
Возьмем какую-нибудь точку из n точек. К скольким точкам можно провести из нее прямую? Так как никакие три из n точек не лежат на одной прямой, то всего будет сделать это. Так как это рассуждение можно сделать с любой из n точек, то мы пока получаем всего возможных сделать это: n(n-1) .
Но нужно учесть, что прямая от точки B до точки А - это тоже самое, что и прямая от точки А до точки В. Поэтому общее количество нужно разделить на 2:
При этом можно провести любое натуральное (0 прямых не считается) число прямых меньше указанного выше числа.
а). Через три точки максимум можно провести:
(рисунок 1)
б). Для четырех точек:
(рисунок 2)
То есть, прямых можно провести любое число от 1 до 6.
в). Для пяти точек максимум равен:
(рисунок 3)
То есть, прямых можно провести любое число от 1 до 10.
То есть всего можно провести 1 прямую, 2 и 3 прямые.
Примечание:
В решении мы пользовались, тем, никакие ТРИ из прямых не лежат на одной прямой (фотография 2).
Расстояние от вершин треугольника до точек касания вписанной окружности равны по теореме о касательных.Обозначим расстояние от вершины угла при основании до точки касания окружности боковой стороны 8х,от этой точки до вершины угла напротив основания 3х( ПО УСЛОВИЮ).Получаем боковая сторона= 11х.Тогда по т-ме о касательной , расстояние от вершины при основании до точки касания окружности с основанием тоже = 8х.Все по той же теореме вторая боковая сторона делится точкой касания на отрезки 8х и 3х, считая от основания, а само основание на отрезки 8х и 8х.Тогда Р= 11х+11х+8х+8х=38х=76 х=2.Значит боковая сторона 11*2=22 ,основание 16*2=32
а). От 1 до 3 прямых.
б). От 1 до 6 прямых.
в). От 1 до 10 прямых.
г). От 1 до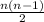 прямых.
прямых.
Объяснение:
г). [Сначала разберем общий случай] Найдем максимальное количество прямых, которое можно провести через определенные n точек, никакие три из которых не лежат на одной прямой.
Возьмем какую-нибудь точку из n точек. К скольким точкам можно провести из нее прямую? Так как никакие три из n точек не лежат на одной прямой, то всего будет сделать это. Так как это рассуждение можно сделать с любой из n точек, то мы пока получаем всего возможных сделать это: n(n-1) .
Но нужно учесть, что прямая от точки B до точки А - это тоже самое, что и прямая от точки А до точки В. Поэтому общее количество нужно разделить на 2:
При этом можно провести любое натуральное (0 прямых не считается) число прямых меньше указанного выше числа.
а). Через три точки максимум можно провести:
б). Для четырех точек:
То есть, прямых можно провести любое число от 1 до 6.
в). Для пяти точек максимум равен:
То есть, прямых можно провести любое число от 1 до 10.
То есть всего можно провести 1 прямую, 2 и 3 прямые.
Примечание:
В решении мы пользовались, тем, никакие ТРИ из прямых не лежат на одной прямой (фотография 2).