у нас ABCD прямоугольник, мы с легкостью найдём его диагональ CA.
рассмотрим треугольник допустим ABC, мы знаем что у него угол B = 90 градусам так как он часть большого прямоугольника, и знаем две его стороны, допустим BC = 3см, а ВА = 6см. По теореме Пифагора найдём гипотенузу СА. СА=см.
теперь рассмотрим треугольник С1СА, он тоже прямоугольный, угол С=90 градусов. Нам известно сколько равно СА, и сколько равна диагональ С1А. По теореме Пифагора найдём высоту СС1. СС1= см. Теперь мы знаем высоту СС1=Н.
Найдём Sбоковую. Sбок= Р(основы)*Н. Р = 3+3+6+6=18см => Sбок = 18*3= 54см^2. Теперь найдём Sосновы. Так как основание прямоугольник, то площадь будет равна произведению сторон Sосновы = 3*6= 18см^2.
и теперь наконец-то вернёмся к полной площади Sполная = 54+2*18= 90см^2.
ку) кр на 176 стр задание 5? :)
го хэлпану :
как мы знаем Sполная = Sбоковая + 2Sосновы.
у нас ABCD прямоугольник, мы с легкостью найдём его диагональ CA.
рассмотрим треугольник допустим ABC, мы знаем что у него угол B = 90 градусам так как он часть большого прямоугольника, и знаем две его стороны, допустим BC = 3см, а ВА = 6см. По теореме Пифагора найдём гипотенузу СА. СА=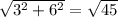
см.
теперь рассмотрим треугольник С1СА, он тоже прямоугольный, угол С=90 градусов. Нам известно сколько равно СА, и сколько равна диагональ С1А. По теореме Пифагора найдём высоту СС1. СС1=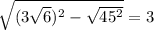
см. Теперь мы знаем высоту СС1=Н.
Найдём Sбоковую. Sбок= Р(основы)*Н. Р = 3+3+6+6=18см => Sбок = 18*3= 54см^2. Теперь найдём Sосновы. Так как основание прямоугольник, то площадь будет равна произведению сторон Sосновы = 3*6= 18см^2.
и теперь наконец-то вернёмся к полной площади Sполная = 54+2*18= 90см^2.
С тебя лайк :)
Объяснение:
Дано:
Угол BAD= угол ADH=90°
BC=16см
АВ=АD
Рассмотрим прямоугольный ∆АВD.
Так как по условию меньшее основание трапеции равно меньшей боковой стороне, тоесть AD=AB, то ∆ADB равнобедренный с основанием BD, следовательно:
угол ADB= углу АВD.
Найдем угол ADB:
В прямоугольном треугольнике сумма острых углов равна 90°, тогда угол ADB=90°:2=45°
Рассмотрим ∆BDC.
Угол DBC=90° (так как по условию диагональ проведённая из тупого угла перпендикулярна большей боковой стороне), следовательно ∆BDC прямоугольный
Угол BDC=угол ADH– угол ADB=90°–45°=45°
Сумма острых углов в прямоугольной треугольнике равна 90°, следовательно угол BCD=90–угол BDC=90°–45°=45°
Получим: угол ВСD = угол BDC, тогда ∆BDC равнобедренный с основанием DC, следовательно BC=BD.
Так как ВС по условию 16 см, то и ВD=16 см.
Проведём высоту BH из угла АВС к стороне DC.
Так как по условию АВ=AD, а угол DAB=90° (прямой угол трапеции), то ABHD — квадрат.
Следовательно: AD=BH=DH
Найдем АD.
По теореме Пифагора BD²=AD²+AB²
16²=2AD²
256=2AD²
128=AD
AD=√128
AD=8√2
Sтрапеции=Sкв+Sтреугольника BHC
Sкв=а²
Где а сторона квадрата
Sкв=(8√2)²=128 см²
Треугольник BHC прямоугольный с прямым углом BHC ( так как BH высота)
Так как угол BCH=45°, то угол HBC=90°–угол BCH=90°–45°=45°
Тогда прямоугольный треугольник BHC равнобедренный.
Площадь прямоугольного равнобедренного треугольника равна половине квадрата стороны, тоесть:
S=0,5*a²
Подставим значения:
S=0,5*(8√2)²=64 см²
Найдем общую площадь:
S=128+64=192 см²
Ртрапеции=AB+AD+DH+HC+BC=8√2+8√2+8√2+8√2+16=4*(8√2)+16=32√2+16 (см)
ответ: S=192 см²
Р=32√2+16 см