Составьте общее уравнение прямой
проходящей через точки А(2; 4) и В(-3;1)

Показать ответ

Ответ:

0THEbigBOOM0

18.02.2023 05:54

Треугольник АВЕ равен треугольнику CDF, т.к. АВ=СД, угол 1=углу 2, как накрест лежащие при параллельных прямых АВ и СД и секущей АС. Треугольники прямоугольные равны по гипотенузе и острому углу. А в равных треугольниках против равных углов лежат равные стороны. Значит BE=FD. Но они ещё и параллельны, как 2 перпендикуляра к одной прямой.
Отсюда треугольники DEF и DEF равны к прямоугольные, по двум катетам. А в равных треугольниках против равных углов лежат равные стороны. Против угла F лежит сторона ЕД против угла Е лежит сторона BF. Значит они равны.
А если в четырехугольнике противолежащие стороны попарно равны, то это параллелограмм. Что и требовалось доказать.

0,0(0 оценок)

Ответ:

mehili

16.12.2021 14:03

1. Известно, что треугольник с искомыми сторонами подобен исходному, то есть все соответственные элементы у треугольников соотносятся как коэффициент подобия.

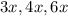Пусть коэффициент подобия равен . Тогда стороны второго треугольника равны 3x,4x,6x . А их сумма, то есть периметр, рана 58,5 см.

Имеем уравнение

$$3x+4x+6x=58,5; 13x=58,5; x=\frac{58,5}{13}=\frac{117}{26}=\frac{9}{2}$

$$3\cdot\frac{9}{2}= \frac{27}{2}=13,5 ; 4\cdot \frac{9}{2}=18; 6\cdot \frac{9}{2}=27$

ответ: 13,5 см, 18 см, 27 см.

2. Сумма углов треугольника равна 180°. Третий угол равен 180°-(54°+18°)=108°

Далее, биссектриса делит угол пополам, то тупой угол будет разбит на два угла по 108°/2=54°

Получится два треугольника (рисунок приложен)

Рассмотрим треугольник, в котором присутствует угол 18° из исходного треугольника (левый на рисунке). Второй угол равен 54°. Но и в исходном треугольнике есть углы 18° и 54°, а это означает, что этот отсеченный треугольник подобен исходному треугольнику (по двум углам). Второй отсеченный треугольник, кстати, является равнобедренным (имеет два угла по 54°).