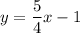Значит, угловой коэффициент этой прямой Обозначим его . Чтобы прямые были перпендикулярны, угловой коэффициент первой прямой и второй (обозначим его ) должны быть связаны соотношением .
Значит, угловой коэффициент искомой прямой равен .
Уравнение прямой, проходящую через точку с угловым коэффициентом , имеет вид . В нашем случае:
Выразим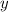 из уравнения прямой:
из уравнения прямой:
Значит, угловой коэффициент этой прямой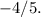 Обозначим его
Обозначим его 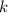 . Чтобы прямые были перпендикулярны, угловой коэффициент первой прямой и второй (обозначим его
. Чтобы прямые были перпендикулярны, угловой коэффициент первой прямой и второй (обозначим его 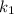 ) должны быть связаны соотношением
) должны быть связаны соотношением 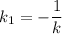 .
.
Значит, угловой коэффициент искомой прямой равен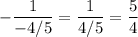 .
.
Уравнение прямой, проходящую через точку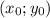 с угловым коэффициентом
с угловым коэффициентом 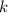 , имеет вид
, имеет вид  . В нашем случае:
. В нашем случае:
ответ: