Поскольку в условиях указана только величина расстояния от центра окружности до прямой, но не указано под каким углом проведена воображаемая линия от центра до прямой, то возможны следующие варианты:
1. Прямая представляет собой касательную к окружности. В этом случае окружность и прямая будут иметь только одну общую точку, расположенную на расстоянии радиуса окружности от ее центра.
2. Прямая может пересекать окружность как угодно. В этом случае мы получим 2 точки пересечения, каждая из которых будет удалена от центра окружности на расстояние радиуса.
1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.
Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора .
Площадь трапеции ANMB равна
Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна
Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна
Поскольку в условиях указана только величина расстояния от центра окружности до прямой, но не указано под каким углом проведена воображаемая линия от центра до прямой, то возможны следующие варианты:
1. Прямая представляет собой касательную к окружности. В этом случае окружность и прямая будут иметь только одну общую точку, расположенную на расстоянии радиуса окружности от ее центра.
2. Прямая может пересекать окружность как угодно. В этом случае мы получим 2 точки пересечения, каждая из которых будет удалена от центра окружности на расстояние радиуса.
1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.
Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора .
.
Площадь трапеции ANMB равна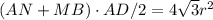
Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна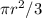
Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна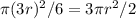
Площадь искомой фигуры