Сторона квадрата дорівнює 6 см. Знайти довжину кола, вписаного в цей квадрат.
2. Сторона правильного шестикутника дорівнює 10 см. Знайти довжину кола, вписаного в цей шестикутник
3. Периметр правильного трикутника дорівнює 36 см. Знайти довжину кола, описаного навколо цього трикутника
4. Скільки сторін у правильного многокутника, якщо його внутрішній кут становить 1350?
5. Сторона правильного шестикутника дорівнює 4 см. Знайти довжину кола, описаного навколо цього шестикутника.
6. Знайти довжину дуги кола в 600, якщо радіус цього кола 16 см.
7. Знайти величину внутрішнього кута правильного 18-кутника
8. Знайти площу кругового сектора, якому відповідає дуга кола у 1200, якщо радіус цього кола 10 см.
9. Знайти величину внутрішнього кута правильного 20-кутника.
10. У правильному шестикутнику менша діагональ дорівнює 8 см. Знайти периметр і більшу діагональ цього шестикутника.
11. Коло розділене на частини, які відносяться як 3:7:8, радіус круга, обмеженого даним колом, дорівнює 8 см. Знайти площу кругового сектора, обмеженого найменшою з утворених дуг.
12. Коло розділене на частини, які відносяться як 4:6:8, радіус круга, обмеженого цим колом, дорівнює 10 см. Знайти площу кругового сектора, обмеженого найбільшою з утворених дуг.

Показать ответ

Ответ:

noeva2005

30.12.2020 15:40

Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

Объяснение:

Рисунок прилагается.

Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.

Найти катеты AC и BC.

Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.

Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.

h² = a₁*b₁ = 2 * 18 = 36; h = 6

⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.

Из прямоугольного ΔACH по теореме Пифагора:

a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10

Катет AC = 2√10 см/

Из прямоугольного ΔBCH по теореме Пифагора:

b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10

Катет BC = 6√10 см.

Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

Проекція катетів прямокутного трикутника 2 і 18 см. Знайти катети

0,0(0 оценок)

Ответ:

МирославаКарповичь

27.03.2022 07:17

Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.

Найти: а) AB; б) CD

Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° =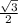 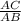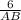$\frac{\sqrt{3}}{2}$ = $\frac{AC}{AB\\}$ = $\frac{6}{AB}$ ; Отсюда AB = 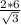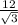$\frac{2*6}{\sqrt{3} }$ = $\frac{12}{\sqrt{3} }$ см.

2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.

ответ: а)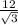 $\frac{12}{\sqrt{3} }\\$ см; б) CD = 3 см.