Дано:
ΔАВС - равнобедренный (АВ и ВС - боковые стороны).
Р(ΔАВС) = 25 см.
Разность двух сторон = 4 см.
Найти:
АВ = ?
ВС = ?
АС = ?
1) Итак, разность боковых сторон АВ и ВС не может быть равна 4 см, так как они равны, и при вычитании должны давать 0.
Тогда, только остаётся, что разность основания АС и боковой стороны АВ = 4 см.
Пусть боковые стороны АВ и ВС = х, а основание АС = у.
Составим систему -
АВ = ВС = х = 7 см.
АС = у = 11 см.
2) Но стоп, вдруг боковая сторона больше основания, тогда получится, что разность боковой стороны АВ и основания АС = 4 см!
Составим новую систему -
АВ = ВС = х = 29/3 см.
АС = у = см.
ответ: 7 см, 7 см, 11 см или 29/3 см, 29/3 см, 5+(2/3) см.
y⃗ =−2x⃗
Произведением вектора a⃗ на число k, (k≠0) называется вектор b⃗ , модуль которого равен |k|⋅|a⃗ |, т.е.,
∣∣b⃗ ∣∣=|k|⋅|a⃗ |, при этом:
- векторы a⃗ и b⃗ сонаправлены, если k>0
- векторы a⃗ и b⃗ противоположно направлены, если k<0
Два ненулевых вектора a⃗ и b⃗ коллинеарны тогда и только тогда, когда существует такое число k, при котором выполняется равенство a⃗ =k⋅b⃗ .
1. На данном рисунке вектор x⃗ умножается на число k, которое равно −2, при этом получаем вектор y⃗ , это можно выразить так: y⃗ =−2x⃗ .
2. Векторы x⃗ и y⃗ коллинеарны, поэтому каждый из них можно выразить как произведение второго вектора на число,
Дано:
ΔАВС - равнобедренный (АВ и ВС - боковые стороны).
Р(ΔАВС) = 25 см.
Разность двух сторон = 4 см.
Найти:
АВ = ?
ВС = ?
АС = ?
1) Итак, разность боковых сторон АВ и ВС не может быть равна 4 см, так как они равны, и при вычитании должны давать 0.
Тогда, только остаётся, что разность основания АС и боковой стороны АВ = 4 см.
Пусть боковые стороны АВ и ВС = х, а основание АС = у.
Составим систему -
АВ = ВС = х = 7 см.
АС = у = 11 см.
2) Но стоп, вдруг боковая сторона больше основания, тогда получится, что разность боковой стороны АВ и основания АС = 4 см!
Составим новую систему -
АВ = ВС = х = 29/3 см.
АС = у =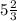 см.
см.
ответ: 7 см, 7 см, 11 см или 29/3 см, 29/3 см, 5+(2/3) см.
y⃗ =−2x⃗
Произведением вектора a⃗ на число k, (k≠0) называется вектор b⃗ , модуль которого равен |k|⋅|a⃗ |, т.е.,
∣∣b⃗ ∣∣=|k|⋅|a⃗ |, при этом:
- векторы a⃗ и b⃗ сонаправлены, если k>0
- векторы a⃗ и b⃗ противоположно направлены, если k<0
Два ненулевых вектора a⃗ и b⃗ коллинеарны тогда и только тогда, когда существует такое число k, при котором выполняется равенство a⃗ =k⋅b⃗ .
1. На данном рисунке вектор x⃗ умножается на число k, которое равно −2, при этом получаем вектор y⃗ , это можно выразить так: y⃗ =−2x⃗ .
2. Векторы x⃗ и y⃗ коллинеарны, поэтому каждый из них можно выразить как произведение второго вектора на число,