5) даны накрестлежащие углы, при параллельных прямых они равны
эти прямые параллельны при условии ∠а=90*, тогда:
180-а=180-90=90*
90=90
При других значениях а равенство не соблюдается, утверждать , что нам дана именно эта градусная мера мы не можем.
6)
∠DKC и ∠АКВ вертикальные - они равны, DK и КВ равны, СК и АК тоже равны, тогда треугольники DKC и АКВ равны по двум сторонам и углу между ними. В равных треугольниках соответствующие элементы также равны - ∠А=∠С ,∠D=∠B .
рассмотрим прямые a,b при секущей BD
∠ВDС=∠DBA - накрестлежащие , они при параллельных прямых равны, мы это доказали .
7) Дан р/б треугольник, в нем углы при основании (МЕ) равны ∠М=∠Е.
Данные нам углы назовем ∠М- внутри треугольника и ∠М1 .
Рассмотрим прямые a,b при секущей МЕ
∠Е=∠М1- накрестлежащие , они при параллельных прямых равны, мы это доказали .
8) Дан р/б треугольник АВС , значит ∠А=∠С=80*
∠КАС =80-40=40*
Рассмотрим треугольник КАР- он р/б
∠КАР=∠КРА=40*
Рассмотрим прямые a,b при секущей АР
∠РАС=∠КРА - накрестлежащие , они при параллельных прямых равны.
Исследуйте, может ли диагональ прямоугольного параллелепипеда составлять с плоскостями двух его смежных боковых граней углы 45 градусов и 60 градусов.
Объяснение:
1)Все грани прямоугольного параллелепипеда - прямоугольники . ΔАВ1D - прямоугольный по т. о трех перпендикулярах : т.к. проекция ВА⊥АD , прямой лежащей в плоскости, то и наклонная АВ1⊥АD, прямой лежащей в плоскости АD⇒∠В1АD=90° .
ΔВ1СD - прямоугольный аналогично.
2) Пусть ∠AB1D=45° ,∠CB1D=60° .
В ΔAB1D , ∠ADB1=45°⇒ равнобедренный и AD=FD1=a. Тогда В1D=√(а²+а²)=а√2.
3)ΔB1CD ,cos 60°=B1C/B1D , B1C=a√2/2.
4) ΔABB1 по т Пифагора h=BB1=√(a²-b²)⇒a>b .
5 )ΔB1CC1 -прямоугольный . по т. Пифагора ,
чего быть не может.
Значит диагональ прямоугольного параллелепипеда составлять с плоскостями двух его смежных боковых граней углы 45 градусов и 60 градусов не может.
5) даны накрестлежащие углы, при параллельных прямых они равны
эти прямые параллельны при условии ∠а=90*, тогда:
180-а=180-90=90*
90=90
При других значениях а равенство не соблюдается, утверждать , что нам дана именно эта градусная мера мы не можем.
6)
∠DKC и ∠АКВ вертикальные - они равны, DK и КВ равны, СК и АК тоже равны, тогда треугольники DKC и АКВ равны по двум сторонам и углу между ними. В равных треугольниках соответствующие элементы также равны - ∠А=∠С ,∠D=∠B .
рассмотрим прямые a,b при секущей BD
∠ВDС=∠DBA - накрестлежащие , они при параллельных прямых равны, мы это доказали .
7) Дан р/б треугольник, в нем углы при основании (МЕ) равны ∠М=∠Е.
Данные нам углы назовем ∠М- внутри треугольника и ∠М1 .
Рассмотрим прямые a,b при секущей МЕ
∠Е=∠М1- накрестлежащие , они при параллельных прямых равны, мы это доказали .
8) Дан р/б треугольник АВС , значит ∠А=∠С=80*
∠КАС =80-40=40*
Рассмотрим треугольник КАР- он р/б
∠КАР=∠КРА=40*
Рассмотрим прямые a,b при секущей АР
∠РАС=∠КРА - накрестлежащие , они при параллельных прямых равны.
Исследуйте, может ли диагональ прямоугольного параллелепипеда составлять с плоскостями двух его смежных боковых граней углы 45 градусов и 60 градусов.
Объяснение:
1)Все грани прямоугольного параллелепипеда - прямоугольники . ΔАВ1D - прямоугольный по т. о трех перпендикулярах : т.к. проекция ВА⊥АD , прямой лежащей в плоскости, то и наклонная АВ1⊥АD, прямой лежащей в плоскости АD⇒∠В1АD=90° .
ΔВ1СD - прямоугольный аналогично.
2) Пусть ∠AB1D=45° ,∠CB1D=60° .
В ΔAB1D , ∠ADB1=45°⇒ равнобедренный и AD=FD1=a. Тогда В1D=√(а²+а²)=а√2.
3)ΔB1CD ,cos 60°=B1C/B1D , B1C=a√2/2.
4) ΔABB1 по т Пифагора h=BB1=√(a²-b²)⇒a>b .
5 )ΔB1CC1 -прямоугольный . по т. Пифагора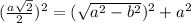 ,
,
Значит диагональ прямоугольного параллелепипеда составлять с плоскостями двух его смежных боковых граней углы 45 градусов и 60 градусов не может.