Запишите уравнение прямой, симметрично прямой y = x - 2 относительно точки A(-3;1)
Объяснение:
Прямая y = x - 2, к=1 ; К(0; -2) принадлежит этой прямой( легко проверяется) .
Пусть уравнение симметричной прямой у₁=к₁х+в₁ .
Т.к прямые симметричные относительно точки, то они параллельны ⇒ их угловые коэффициенты равны , значит к₁=1. Пусть К₁∈у₁ .
Найдем координаты точки К₁(х;у) симметричной точке К( 0;-2) относительно A(-3;1) , по формулам середины отрезка ( тк.АК=АК₁)
х(А)= , x(K₁)=-3*2-0=-6,
y(A)= , y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
В уравнение у₁=к₁х+в₁ подставим к=1 и K₁(-6; 4 ) , получим 4=1*(-6)+в₁,
в₁=10 . Окончательно получаем у₁=1х+10 или у₁=х+10.
Sосн=36см²
Sбок=224см²
Sпол=296см²
V=288cм³
Дано
ABCDA1B1C1D1- призма
ABCD- трапеция
АВ=CD=5см боковая сторона трапеции.
ВС=6см верхнее основание трапеции.
АD=12см нижнее основание трапеции.
В1В:ВК=2:1.
Sосн.=?
Sбок=?
Sпол=?
V=?
Решение.
АК=МD
AK=(AD-BC)/2=(12-6)/2=6/2=3 см.
∆АВК- прямоугольный (<ВКА=90°)
По теореме Пифагора найдем высоту трапеции.
ВК²=АВ²-АК²=5²-3²=25-9=16см.
ВК=√16=4 см высота трапеции.
Sосн=ВК(ВС+AD)/2=4*(6+12)/2=4*18/2=
=36см² площадь трапеции.
ВВ1=2*ВК=2*4=8см высота призмы.
Росн=АВ*2+ВС+AD=5*2+6+12=10+18=28см периметр трапеции.
Sбок=Росн*ВВ1=28*8=224см² площадь боковой поверхности призмы.
Sпол=2Sосн+Sбок=2*36+224=72+224=
=296 см² площадь полной поверхности призмы.
V=Sосн*ВВ1=36*8=288см³ объем призмы.
Запишите уравнение прямой, симметрично прямой y = x - 2 относительно точки A(-3;1)
Объяснение:
Прямая y = x - 2, к=1 ; К(0; -2) принадлежит этой прямой( легко проверяется) .
Пусть уравнение симметричной прямой у₁=к₁х+в₁ .
Т.к прямые симметричные относительно точки, то они параллельны ⇒ их угловые коэффициенты равны , значит к₁=1. Пусть К₁∈у₁ .
Найдем координаты точки К₁(х;у) симметричной точке К( 0;-2) относительно A(-3;1) , по формулам середины отрезка ( тк.АК=АК₁)
х(А)=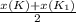
, x(K₁)=-3*2-0=-6,
y(A)=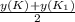
, y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
В уравнение у₁=к₁х+в₁ подставим к=1 и K₁(-6; 4 ) , получим 4=1*(-6)+в₁,
в₁=10 . Окончательно получаем у₁=1х+10 или у₁=х+10.
Sосн=36см²
Sбок=224см²
Sпол=296см²
V=288cм³
Объяснение:
Дано
ABCDA1B1C1D1- призма
ABCD- трапеция
АВ=CD=5см боковая сторона трапеции.
ВС=6см верхнее основание трапеции.
АD=12см нижнее основание трапеции.
В1В:ВК=2:1.
Sосн.=?
Sбок=?
Sпол=?
V=?
Решение.
АК=МD
AK=(AD-BC)/2=(12-6)/2=6/2=3 см.
∆АВК- прямоугольный (<ВКА=90°)
По теореме Пифагора найдем высоту трапеции.
ВК²=АВ²-АК²=5²-3²=25-9=16см.
ВК=√16=4 см высота трапеции.
Sосн=ВК(ВС+AD)/2=4*(6+12)/2=4*18/2=
=36см² площадь трапеции.
ВВ1=2*ВК=2*4=8см высота призмы.
Росн=АВ*2+ВС+AD=5*2+6+12=10+18=28см периметр трапеции.
Sбок=Росн*ВВ1=28*8=224см² площадь боковой поверхности призмы.
Sпол=2Sосн+Sбок=2*36+224=72+224=
=296 см² площадь полной поверхности призмы.
V=Sосн*ВВ1=36*8=288см³ объем призмы.