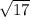1. Против угла 30° лежит катет в два раза меньше гипотенузы ⇒ ВС=10/2=5 ед.
2. ΔАВС равнобедренный (углы 90, 45 и 45). CD - высота, биссектриса и медиана проведенные из вершины равнобедренного, прямоугольного треугольника. Медиана, проведенная из прямого угла треугольника равна половине его гипотенузы. ⇒ АВ=8*2=16 ед.
3. ЕС - катет прямоугольного треугольника ЕВС лежащий против угла 30° ⇒ ЕВ=7*2=14. По т. Пифагора ВС=√(14²-7²)=√147. ВС - катет прямоугольного треугольника АВС лежит против угла 30° ⇒АВ=2√147. По т. Пифагора АС=√((2*147)²-(√147)²)=21.
1. Против угла 30° лежит катет в два раза меньше гипотенузы ⇒ ВС=10/2=5 ед.
2. ΔАВС равнобедренный (углы 90, 45 и 45). CD - высота, биссектриса и медиана проведенные из вершины равнобедренного, прямоугольного треугольника. Медиана, проведенная из прямого угла треугольника равна половине его гипотенузы. ⇒ АВ=8*2=16 ед.
3. ЕС - катет прямоугольного треугольника ЕВС лежащий против угла 30° ⇒ ЕВ=7*2=14. По т. Пифагора ВС=√(14²-7²)=√147. ВС - катет прямоугольного треугольника АВС лежит против угла 30° ⇒АВ=2√147. По т. Пифагора АС=√((2*147)²-(√147)²)=21.
АЕ=АС - ЕС=21-7=14 ед.
Найдем вектора, соответствующие сторонам этого треугольника:
AB = B-A = (1,4)
BC = C-B = (3,-3)
AC = C-A = (4,1)
Найдем длины векторов:
|AB| =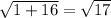
|BC| =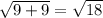
|AC| =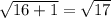
Нетрудно видеть, что |AB| = |AC|
Следовательно треугольник равнобедренный.
Найдем скалярное произведение векторов и проверим, является ли треугольник прямоугольным:
AB*BC = (3-12) = -9
BC*AC = 12-3 = -9
AB*AC = 4+4 = 8
Скалярное произведение векторов ни в одном случае не равно нулю, следовательно треугольник не является прямоугольным.
ответ: Треугольник равнобедренный, равные стороны: AB = AC =