Сума проекцій катетів прямокутного трикутника на гіпотенузу дорівнює 25 см, а висота, проведена з вершини прямого кута, дорівнює 12 см. Обчисти периметр трикутника

Показать ответ

Ответ:

tural23

24.10.2022 05:34

1. 4) такого тр-ка не существует, потому-что 5+9<15, а с таким отношением тр-ник построить нельзя.
2. Пусть боковые стороны будут a=х и b=х-3.
Так как высота делит тр-ник на два прямоугольных тр-ка и она для них общая, то по т. Пифагора можно записать ур-ние:
х²-10²=(х-3)²-5²,
х²-100=х²-6х+9-25,
х=14,
а=14 см, b=14-3=11 см, c=5+10=15 cм.
Р=14+11+15=40 см.
ответ: б) 40 см.
3. АВСД - ромб, ∠А=60°, АВ=АД, значит АВД - правильный тр-ник. В нём АО - высота. АО=АВ√3/2, АС=2АО=АВ√3 ⇒ АВ=АС/√3.
АВ=4√3/√3=4 см.
Периметр ромба: Р=4АВ=16 см.
ответ: а) 16 см.

0,0(0 оценок)

Ответ:

Wertwer123

23.09.2021 19:05

Чертеж к решению - во вложении.

Т.к. О - центр вписанной в ΔАВС окружности, то О - точка пересечения биссектрис углов ΔАВС. Значит, АО и ВО - биссектрисы.

Т.к. О1 - центр внеписанной окружности то О1 - точка пересечения биссектрис внешних углов ΔАВС. Значит, АО1 и ВО1 - биссектрисы.

Пусть α - величина внешнего угла ΔАВС при вершине А, тогда (180°-α) - величина внутреннего угла ΔАВС при вершине А, т.к. эти углы - смежные.

Тогда

$\angle\ O_1AB=\frac{\alpha }{2};\ \angle\ OAB=\frac{180^0-\alpha}{2} =90^0-\frac{\alpha }{2};\\ \Rightarrow \angle OAO_1= \angle OAB+ \angle O_1AB=\frac{\alpha }{2}+(90^0-\frac{\alpha }{2})=90^0$

Аналогично,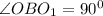 $\angle OBO_1=90^0$

Рассмотрим четырехугольник АОВО1.

У него сумма противолежащих углов А и В равна 90°+90° = 180°.

Т.к. сумма всех углов этого выпуклого четырехугольника равна 360°, то сумма двух других противолежащих при вершинах О и О1 также равна 180°.

Таким образом, воспользуемся утверждением: если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Делаем вывод, точки А, В, О и О1 лежат на одной окружности.

Доказано.