рассмотрим треугольник АОС, он - равнобедренный ( это следует из 1)
треугольник ДОВ, так же равнобедренный ( из 1)
между пересечениями этих линий у нас образовались равные углы: угол АОС= углу ДОВ ( они вертикальные) (2), и также угол СОД=углу СОВ (они тоже вертикальные) (3)
=> треугольник АОС = треугольнику ДОБ (по 1ому признаку: если две стороны одного треугольника и угол между ними равны двум сторонам и углу между ними соответственно, то такие треугольники равны) следовательно АС=ВД, треугольник АОД=СОВ (по 1ому признаку)следовательно АД=СВ
в итоге имеем прямоугольник (четырехугольник у которого две стороны попарно равны - прямоугольник) следовательно Ас параллельно ДВ ( по признаку прямоугольника) что и требовалось доказать
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
из дано следует, что АО=СО=ВО=DО (1)
рассмотрим треугольник АОС, он - равнобедренный ( это следует из 1)
треугольник ДОВ, так же равнобедренный ( из 1)
между пересечениями этих линий у нас образовались равные углы: угол АОС= углу ДОВ ( они вертикальные) (2), и также угол СОД=углу СОВ (они тоже вертикальные) (3)
=> треугольник АОС = треугольнику ДОБ (по 1ому признаку: если две стороны одного треугольника и угол между ними равны двум сторонам и углу между ними соответственно, то такие треугольники равны) следовательно АС=ВД, треугольник АОД=СОВ (по 1ому признаку)следовательно АД=СВ
в итоге имеем прямоугольник (четырехугольник у которого две стороны попарно равны - прямоугольник) следовательно Ас параллельно ДВ ( по признаку прямоугольника) что и требовалось доказать
удач
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их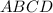 и
и 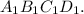
Проведём диагональ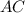 в квадрате
в квадрате 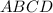 и диагональ
и диагональ 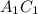 в квадрате
в квадрате 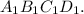
Рассмотрим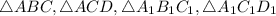 .
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.