точка М лежить ВС рівнобедреного трикутника АВС. Знайдіть площу цього трикутника,якщо його бічні сторони АВ і АС дорівнюють 13 см, а відстаньвід точки М до цих сторін відповідно 8см і 2 см
У параллелограмма всего 4 угла. В параллелограмме есть пара острых равных между собой углов, а также пара равных тупых углов (случай прямоугольника опустим, у него все углы равны, в этой задаче такого нет). Поэтому если мы найдем острый угол, а также тупой угол параллелограмма, то мы нашли все углы.
Теперь найдем их Ситуация следующая: есть две параллельные прямые, каждая из смежных с ними сторон является секущей. Получается, что имеются две пары односторонних друг для друга углов. Рассмотрим любую из них (для второй все то же самое)
Пусть - острый угол, - тупой. Тогда имеет место соотношение
Известно, что сумма односторонних углов равна 180°, получаем вот такое уравнение:
ответ: 6√5 см
Объяснение:
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
По формуле Герона
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см
У параллелограмма всего 4 угла. В параллелограмме есть пара острых равных между собой углов, а также пара равных тупых углов (случай прямоугольника опустим, у него все углы равны, в этой задаче такого нет). Поэтому если мы найдем острый угол, а также тупой угол параллелограмма, то мы нашли все углы.
Теперь найдем их Ситуация следующая: есть две параллельные прямые, каждая из смежных с ними сторон является секущей. Получается, что имеются две пары односторонних друг для друга углов. Рассмотрим любую из них (для второй все то же самое)
Пусть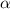 - острый угол,
- острый угол, 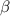 - тупой. Тогда имеет место соотношение
- тупой. Тогда имеет место соотношение
Известно, что сумма односторонних углов равна 180°, получаем вот такое уравнение:
ответ: 72°, 72°, 108°, 108°