Точка N лежит на отрезке MK, MK: NK = 6: 5. Точка C лежит на плоскости a. Сечение NL, параллельное плоскости а, равно 10 см. Прямая ML пересекает плоскость a в точке S. Следуя диаграмме, найдите длину отрезка KЅ.

Показать ответ

Ответ:

У4КГРВ

22.08.2020 01:12

ответ:

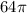$64\pi$ см³.

Объяснение:

Обозначим данную пирамиду буквами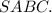 SABC.

AB = 12 см.

Проведём высоту пирамиды SO.

$\angle SAO = 30^{\circ}$

Начертим около этой пирамиды конус.

Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.

=======================================================

Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.

$\Rightarrow AB = BC = AC = 12$ см.

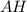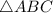
Проведём высоту в $\triangle ABC$

$\triangle SAO$ - прямоугольный, так как - высота пирамиды.

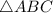$\triangle ABH$ - прямоугольный, так как - высота $\triangle ABC$ .

Так как $\triangle ABC$ - равносторонний ⇒ 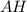- высота, медиана и биссектриса

BH = HC = BC:2 = 12:2 = 6 см, так как - медиана.

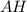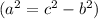Найдём по теореме Пифагора (a^2 = c^2 - b^2) .

$AH = \sqrt{AB^2 - BH^2} = \sqrt{12^2 - 6^2} = \sqrt{108} = 6\sqrt{3}$ см.

Точка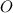 - пересечение медиан и делит их в отношении 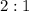2:1 , считая от вершины.

$\Rightarrow AO = 2/3\cdot AH = 2/3 \cdot 6\sqrt{3} = 4\sqrt{3}$ см

$OH = 1/3\cdot AH = 1/3 \cdot 6\sqrt{3} = 2\sqrt{3}$ см.

Также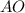 - радиус описанной около 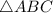$\triangle ABC$ окружности.

Рассмотрим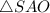 $\triangle SAO$

Если угол в прямоугольном треугольнике равен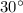 $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow SA = 2SO$

Составим уравнение:

Пусть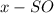 x - SO , тогда 2x - SA .

И по теореме Пифагора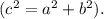 (c^2 = a^2 + b^2).

$(4\sqrt{3})^2 + x^2 = (2x)^2\\\\48 + x^2 = 4x^2\\\\-3x^2 =-48\\\\x^2 =16 \\\\x= 4$

конуса = $1/3 \cdot \pi \cdot AO^2 \cdot SO = \pi \Big(1/3 \cdot (4\sqrt{3})^2 \cdot 4\Big) = 64\pi$ см³.

Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к пл

0,0(0 оценок)

Ответ:

коко60

21.04.2021 18:58

Ptkem = 16 см.

объяснение:

В условии допущена описка.Площадь измеряется в кавдратных единицах, следовательно, площадь грани тетраэдра равна

S = 16√3 см².

Тетраэдр называется правильным, если все его грани - равносторонние треугольники. Тогда сторону тетраэдра найдем из формулы площади правильного треугольника:

S = (√3/4)*a², где а - сторона треугольника.

а² = 4*S/√3 = 4*16√3/√3 = 64 см² => a = 8см.

Точки T,K, и Е - середины ребер DB, DC и AC соответственно, следовательно, отрезки ТК и КЕ - средние линии треугольников - граней тетраэдра BDC и СDA и равны половинам сторон ВС и AD.

Построим сечение тетраэдра плоскостью ТКЕ. Плоскость BDC пересекается плоскостью TKE по линии ТК, параллельной прямой ВС. Но прямая ВС принадлежит и плоскости АВС. Следовательно, плоскость АВС пересечется плоскостью ТКЕ, проходящей через точку Е по прямой ЕМ, параллельной прямой ВС, а отрезок ЕМ является средней линией треугольника АВС. ЕМ = 4см. Соединив точки Т и М (середины сторон АВ и BD), получим сечение тетраэдра плоскостью ТКЕ - четырехугольник ТКЕМ, все стороны которого равны между собой и равны 4 см.

Периметр сечения Ptkem = 4*4 = 16 см.

0,0(0 оценок)

Популярные вопросы: Геометрия