Точка пересечения O — серединная точка для обоих отрезков KG и TM. Как исполняется первый признак равенства треугольников KOT и GOM? 1. сторона TO в треугольнике KOT равна стороне:___ в треугольнике:___ .
2. Сторона KO в треугольнике KOT равна стороне:___ в треугольнике:___ .
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC , ,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC ,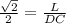
,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
И ΔВCD-равнобедренный ⇒ВD=DС=L√2.
Значит АВ=2L√2.
S=1/2*a*h , S(АВС)=1/2*2L√2*L√2=2L² .
№2
Треугольник КВН-прямоугольный:
По теореме о сумме острых углов прямоугольн. треугольника : 90°-32°=58°-угол КМН.
РАССМОТРИМ треугольник КМТ-прямоугольный:
По теореме о сумме острых углов прямоугольного треугольника : 90°-58°=32°-КНТ.
№3 Рассмотрим треугольник АСВ-прямоугольный:
Угол В=26°,найдем угол А
По теореме о сумме острых углов прямоугольного треугольника :
90°-26°=64°-угол А
АК-биссектриса, высота, медиана и делит угол А пополам.
64°:2=32°-угол САК и угол КАВ.
РАССМОТРИМ треугольник САК-прямоугольный:
По теореме о сумме острых углов прямоугольного треугольника :
90°-32°=58°-УГОЛ АКС.
№9 не знаю)