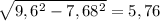расстояние от дома до места, где рассыпано зерно, составляет 8 м.
Объяснение:
Если голуби, стартовавшие синхронно и с одинаковой скоростью, долетели до зерна одновременно, значит, образованные фонарем, домом, землей и траекторией полета голубей два прямоугольных треугольника будут иметь равные гипотенузы (траектории полета голубей).
У одного треугольника катеты будут соответственно равны высоте дома (15 м) и отрезку земли до места, где Анна рассыпала зерно, обозначим его Х м.
У другого треугольника катеты будут соответственно равны высоте фонарного столба (8 м) и отрезку земли до места, где Анна рассыпала зерно:
23 - Х м.
Так как гипотенузы треугольников равны, то на основании теоремы Пифагора, согласно которому квадрат гипотенузы равен квадрату катетов, можно составить уравнение:
расстояние от дома до места, где рассыпано зерно, составляет 8 м.
Объяснение:
Если голуби, стартовавшие синхронно и с одинаковой скоростью, долетели до зерна одновременно, значит, образованные фонарем, домом, землей и траекторией полета голубей два прямоугольных треугольника будут иметь равные гипотенузы (траектории полета голубей).
У одного треугольника катеты будут соответственно равны высоте дома (15 м) и отрезку земли до места, где Анна рассыпала зерно, обозначим его Х м.
У другого треугольника катеты будут соответственно равны высоте фонарного столба (8 м) и отрезку земли до места, где Анна рассыпала зерно:
23 - Х м.
Так как гипотенузы треугольников равны, то на основании теоремы Пифагора, согласно которому квадрат гипотенузы равен квадрату катетов, можно составить уравнение:
с2 = 152 + Х2 = 82 + (23 – Х) 2;
152 + Х2 = 82 + 232 – 2 * 23 * Х + Х2;
152 + Х2 = 82 + 232 – 2 * 23 * Х + Х2;
152 = 82 + 232 – 2 * 23 * Х;
225 = 64 + 529 – 46 * Х;
46 * Х = 64 + 529 – 225;
46 * Х = 368;
Х = 368 : 46;
Х = 8.
Объяснение:
Итак, по условию известно, что косинус угла A равен 0,6
Что такое косинус? Косинус - это отношение прилежащего угла к гипотенузе.
То есть, cos<A = AC/AB (AC является прилежащим катетом по отношению к углу A, AB - гипотенуза).
Тогда AC/AB = 6/10
AB = 12
AC/12 = 6/10
Тогда по свойству пропорции можем найти AC: 12 * 6 : 10 = 7,2 см
Гипотенуза известна, один катет известен, а второй катет - нет.
Второй катет находим по теореме Пифагора:
BC =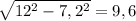
CH - высота треугольника ABC, данная сторона находится в прямоугольном треугольнике HBC
Известен катет(в прямоугольном треугольнике HBC - гипотенуза) BC, BH нам неизвестно.
Обозначим BH и AH ac и bc соответственно.
Воспользуемся формулой:
a =
Где a - это катет BC, с - гипотенуза ABC, ac - это отрезок BH.
a известно, с известно, как найти ac?
Возведем обе части уравнения в квадрат. Получим:
a^2 = c * ac
Откуда ac = a^2 / c = 9,6^2/12 = 92,16/12 = 7,68
Итак, в прямоугольном треугольнике HBC нам уже известно две стороны. Найдем катет CH по теореме Пифагора:
CH =