DO и CD₁ - скрещиваются, но А₁В ║ CD₁ ⇒ угол между прямыми DO и CD₁ равен углу между прямыми DO и А₁В. Пусть ребро исходного куба равно единице: АВ = 1, тогда диагональ грани равна корню из двух: А₁В = √2. Рассмотрим ΔDАO – прямоугольный (DА ⊥ АO), по теореме Пифагора: DO² = АO² + DА², АО = 0,5*АВ₁ = ⇒
DO² = .
Далее рассмотрим ΔDOВ, где ∠DOВ = углу между прямыми DO и А₁В =
= углу между прямыми DO и CD₁. При этом DВ = √2 как диагональ квадрата с единичной стороной, ОВ = , DO² = .
По теореме косинусов: DВ² = DO² + ОВ² – 2 · DO · ОВ · сos(∠DOВ) ⇒
Осевое сечение усеченного конуса - равнобедренная трапеция. основания: а=22 см (R₁*2), b=32 см (R₂*2) боковая сторона - образующая конуса l =13 см найти высоту равнобедренной трапеции - расстояние от центра верхнего основания до центра нижнего основания усеченного конуса перпендикуляры от верхнего основания до нижнего(из тупых углов) отсекают от равнобедренной трапеции 2 равных прямоугольных треугольника с гипотенузой(образующая конуса) 13 см и катетом 5 см ((32-22)/2=10/2=5 см). найти катет -H высоту усеченного конуса. по теореме Пифагора: 13²=5²+H². H²=169-25. H=12 cм ответ: расстояние между центрами оснований усеченного конуса 12 см
DO и CD₁ - скрещиваются, но А₁В ║ CD₁ ⇒ угол между прямыми DO и CD₁ равен углу между прямыми DO и А₁В. Пусть ребро исходного куба равно единице: АВ = 1, тогда диагональ грани равна корню из двух: А₁В = √2. Рассмотрим ΔDАO – прямоугольный (DА ⊥ АO), по теореме Пифагора: DO² = АO² + DА², АО = 0,5*АВ₁ =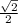 ⇒
⇒
DO² =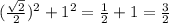 .
.
Далее рассмотрим ΔDOВ, где ∠DOВ = углу между прямыми DO и А₁В =
= углу между прямыми DO и CD₁. При этом DВ = √2 как диагональ квадрата с единичной стороной, ОВ =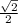 , DO² =
, DO² = 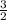 .
.
По теореме косинусов: DВ² = DO² + ОВ² – 2 · DO · ОВ · сos(∠DOВ) ⇒
√2² =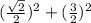
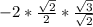 * сos(∠DOВ) ⇒
* сos(∠DOВ) ⇒
√3*сos(∠DOВ) =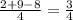 ⇒ сos(∠DOВ) =
⇒ сos(∠DOВ) = 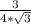 =
= 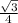 ⇒
⇒
∠DOВ = углу между прямыми DO и CD₁ = arccos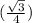
основания:
а=22 см (R₁*2), b=32 см (R₂*2)
боковая сторона - образующая конуса l =13 см
найти высоту равнобедренной трапеции - расстояние от центра верхнего основания до центра нижнего основания усеченного конуса
перпендикуляры от верхнего основания до нижнего(из тупых углов) отсекают от равнобедренной трапеции 2 равных прямоугольных треугольника с гипотенузой(образующая конуса) 13 см и катетом 5 см ((32-22)/2=10/2=5 см). найти катет -H высоту усеченного конуса.
по теореме Пифагора: 13²=5²+H². H²=169-25. H=12 cм
ответ: расстояние между центрами оснований усеченного конуса 12 см