Точки A и C расположены по одну сторону от прямой, к которой от обеих точек проведены перпендикуляры AB и CD равной длины. Определи величину угла∡ABC, если ∡ADB = 18°.

Показать ответ

Ответ:

Азазин

23.03.2020 11:45

Две стороны треугольника равны 4√2 см и 1 см, а третья сторона в √2 раз больше радиуса окружности описанного вокруг треугольника. Найти эту сторону. Сколько решений имеет задача?

Объяснение:

Пусть АВ=4√2 см, АС=1 см , ВС=√2*R.

1) S( треуг) = ( авс): 4R , тогда S(ΔАВС)= ( 4√2*1*√2*R): 4R= 2 (cм²).

С другой стороны S( треуг.) = 1/2*а*в*sin α ⇒ 2=1/2*4√2*1*sin α ,

sin α=√2/2 и ∠ВАС=45° , если угол острый или ∠АВС=135° , если тупой .

2) По т косинусов , если ∠АВС=45° :

ВС²=(4√2)²+1²-2*4√2*1*sin 45°, ВС=5 см;

По т косинусов , если ∠АВС=135° : ВС²=(4√2)²+1²-2*4√2*1*sin 135°,

ВС=33+8√2*(√2/2)=33+8=41 , ВС=√41 см.

0,0(0 оценок)

Ответ:

jhghjlkuyfjy

30.08.2021 22:15

Разложите вектора а,b,с по координатным векторам i , j

Объяснение:

Любой вектор на плоскости можно представить в виде суммы или разности векторов.

Если вектор а можно представить в виде $\displaystyle \vec{a} =x* \displaystyle \vec{i} +y*\displaystyle \vec{j}$ ,где х,у числа , то координаты вектора $\displaystyle \vec{a} (x;y)$

1) Вектор а равен сумме 2-х векторов j, тк направления совпадают , длина вектора а в 2 раза больше : 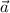$\displaystyle \vec{a} =2\displaystyle \vec{j}$ , $\displaystyle \vec{a}$ (0:2).

2)По клеточкам нарисуем треугольник , так чтобы вектор b был стороной этого треугольника. Выразим вектор b по правилу треугольника : сектор b=АВ+ВС.

Но 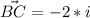$\displaystyle \vec{AB} =-2*\displaystyle \vec{j} ,$ $\displaystyle \vec{BC} =-2*i$ ⇒ $\displaystyle \vec{b} = -2\vec{i} +( -2\vec{j} )$ , координаты b(-2;-2).

3)Вектор с равен вектору -i , тк направления не совпадают , длина вектора c равна длине вектора i :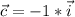 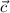$\displaystyle \vec{c} =-1*\displaystyle \vec{i}$ , $\displaystyle \vec{c}$ (-1:0).